用于轨道角动量模式和偏振复用信道交叉连接的级联分区相位调制
专家视点
多维轨道角动量模式复用为扩大通信容量和建立综合网络提供了一条有前景的途径。尽管多维复用取得了一些进展,但这些复用信道的交叉连接,特别是涉及模式和偏振的交叉连接,仍面临挑战,因需要进行多模态互换和按需偏振控制。在此,Zeng和Zhang等人提出了一种通过串级分区相位调制实现轨道角动量模式与偏振交叉变换的解决方案,使得彼此分离的轨道角动量模式能够在不同的空间区域独立施加相位,从而实现模式和偏振信道的协同转换。在实验中,研究人员实现了3个轨道角动量模式与两个偏振复用信道的交叉连接,达到的模式纯度超过0.951,偏振对比度高达0.947。测得的模式插入损耗和偏振转换损耗分别低于3.42 dB和3.54 dB。因此,交换了1.2 Tb/s的四相移键控信号,误码率接近10-6。结合增加的分区相位处理,该方法在容纳大量模式偏振复用信道方面显示出潜力,可能增强大规模轨道角动量模式复用通信网络的网络能力。该工作发表在Optics Letters上。

Qingji Zeng, Bowei Zhang, Shu Chen, Haisheng Wu, Zhibin Wu, Huapeng Ye, Xinxing Zhou, Ze Dong, Junmin Liu, Dianyuan Fan, and Shuqing Chen, Cascaded partitioned phase modulation for cross-connection of orbital angular momentum mode and polarization multiplexing channels, Opt. Lett. 49(16): 4759-4762 (2024).
具有轨道角动量的涡旋光束在利用其模式正交性提供可用复用信道方面,具有显著的潜力,可以扩大通信容量密度并构建高速鲁棒的网络。由于轨道角动量模式独立于偏振和波长的物理维度,其复用在通过与偏振分复用和波长分复用相结合的多维复用方面展现出前景。尽管研究人员揭示了偏振涡旋光栅和多相平面光转换等多维复用的研究成果,但在网络节点上交叉连接这些复用信道以实现数据交换和信息互联是建立通信网络的关键。然而,有效的多维复用信道交叉连接,特别是涉及模式和偏振的交叉连接,面临挑战,因为在多模态互换和按需偏振控制方面存在局限。目前的方法依赖于通过空间光调制器或Pancharatnam-Berry相位设备实现的螺旋相位调制,建立模式映射关系,从而实现双通道模式交叉连接。尽管多个组件的级联可以实现多模态互换,但包括空间光调制器的偏振敏感性和Pancharatnam-Berry相位器件的自旋依赖轨道相互作用导致固定的输入输出偏振响应,这限制了其处理偏振复用信道的能力,从而阻碍了轨道角动量模式与偏振的混合交叉连接的可能性。因此,探索有效的轨道角动量模式与偏振复用信道的交叉连接策略显得尤为紧迫,有望重塑通信网络能力。
研究中,研究人员通过提出一种采用串级分区相位调制的轨道角动量模式与偏振交叉变换策略,解决了这些挑战。由于轨道角动量模式在不同阶数上具有不同的发散特性,它们的复用信道将占据匹配的空间轨迹,从而在自由空间同轴传播中表现出模式的径向空间分离。通过区域位移设计产生的分区相位为多个相位轮廓提供了径向混合布局,明确划分了它们的工作区域。这一结构使得在不同空间区域内对彼此分离的轨道角动量模式进行独立的螺旋相位调制,从而实现多模态互换。与以前通过级联均匀螺旋相位处理大量轨道角动量信道交叉连接的方法相比,这种分区处理在减少级联组件方面具有优势,因为多个区域的并行模式处理降低了系统复杂性。此外,可以通过操控分区调制下线性偏振分量的相位差,选择性地调节特定模式信道的偏振状态。因此,利用分区相位调制的级联部署,可以实现轨道角动量模式与偏振的协同交叉变换,进而实现模式和偏振复用信道的交叉连接。
为了验证方法的可行性,研究人员采用了三层级联相位调制,结合了两个分区相位,证实了其在轨道角动量模式与偏振复用信道交叉连接中的有效性。实验中,研究人员实现了3个轨道角动量模式与两个偏振复用信道的交叉变换,模式纯度超过0.951,偏振对比度高于0.947。因此,研究人员构建了一个24通道的轨道角动量模式数据交换通信系统,结合了三种依赖偏振的轨道角动量模式和八种波长,从中交叉连接了1.2 Tb/s的四相移键控信号,误码率低于10-6。研究人员进一步通过改变输入输出偏振映射和增加交叉连接通道的数量来探讨方法的可扩展性。结果表明,这种交叉连接方法通过增加分区相位调制,释放了容纳大量模式偏振复用信道的潜力。这些结果突显了所提策略在交叉连接轨道角动量模式与偏振信道方面的能力,这为增强网络能力并促进轨道角动量模式复用通信网络中的复杂光节点互连提供了前景。
利用适当的螺旋相位调制进行模式场变换,可以重新定义输出轨道角动量模式的阶数。与此同时,由于模式在不同阶数上的发散特性,这为通过引入分区螺旋相位调制来实现空间分离的轨道角动量模式的多模态变换提供了思路。如图1(a)所示,对于两个复用的轨道角动量模式(分别为|−4⟩和|0⟩),模式的发散导致它们的复合输入模式场不完全重叠。因此,每个模式在进行分区螺旋相位调制后经历相应的移位操作。具体而言,|−4⟩阶的轨道角动量模式在外围区域施加了螺旋相位exp(iφ1),而|0⟩阶的轨道角动量模式在中心区域施加了螺旋相位exp(iφ2)。这里φ1=2θ,φ2=−4θ,θ是方位角。通过这种方式,这两个复用的轨道角动量模式完成了独立的相位调制(|−4⟩·exp(i2θ)和|0⟩·exp(−i4θ)),输出模式的阶数转换为|−2⟩和|−4⟩。
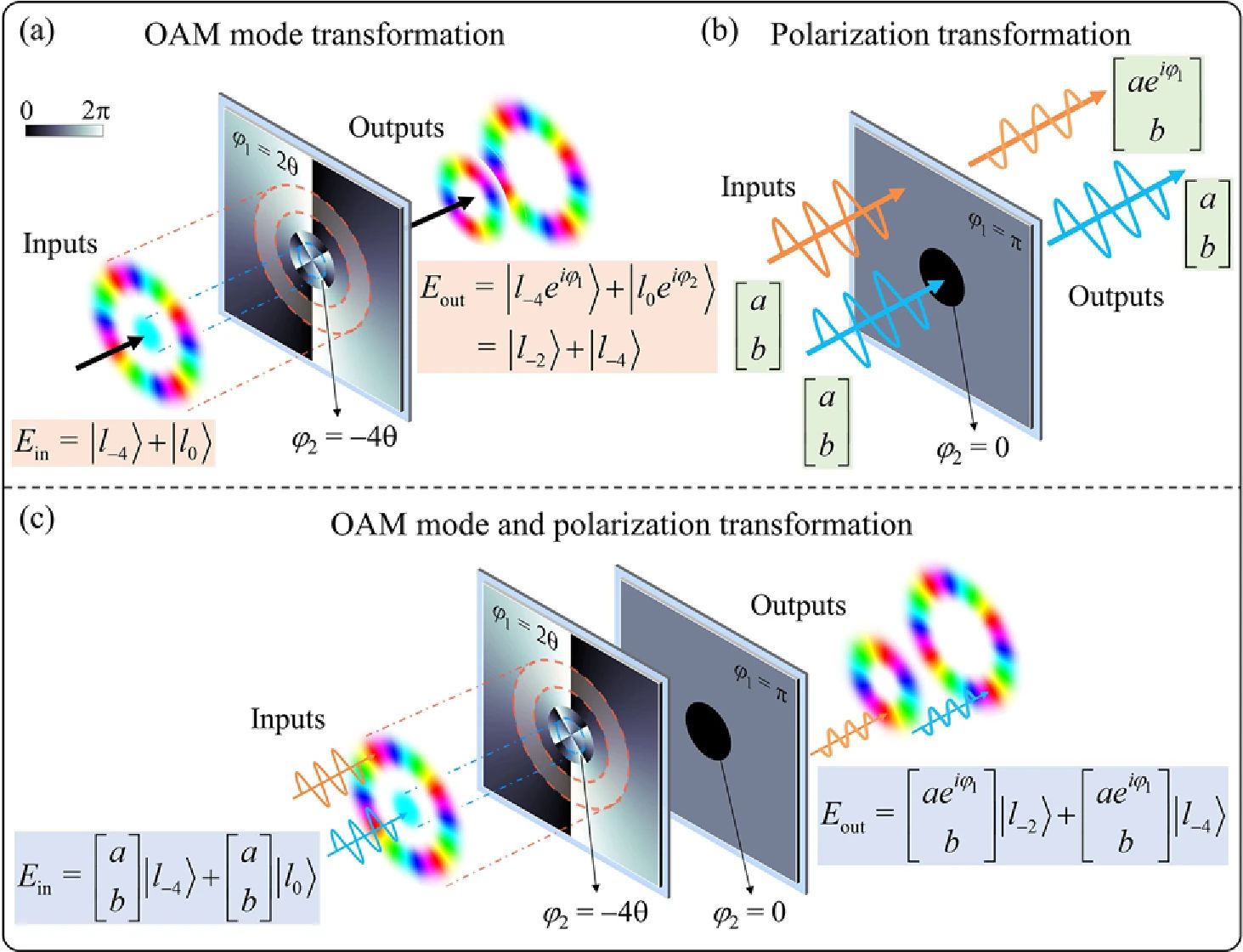
图1 原理。(a) 轨道角动量模式变换,(b) 偏振变换,(c) 采用分区相位调制的轨道角动量模式与偏振变换。
由于光的偏振格式依赖于其在x轴和y轴方向上的相位差,因此对两个正交线性偏振分量进行差分相位调制可以引发偏振转换。如图1(b)所示,对于偏振格式为[a b]的入射光束(T表示矩阵转置运算符),其输出通过引入对x方向敏感的分区恒定相位调制实现偏振变换和偏振保持。在中心区域的相位值为零时,输出光束的偏振状态保持不变。而在外围区域,对其x偏振分量施加额外的恒定相位exp(iπ),使输出偏振状态发生翻转。因此,通过级联这两种类型的分区相位,复用的承载偏振的轨道角动量模式不仅能够完成模式变换,还能实现偏振变换(图1(c))。
为了验证上述原理的可行性,研究人员构建了实验装置用于轨道角动量模式与偏振的混合交叉连接,涉及三个依赖偏振的轨道角动量信道,如图2所示。为了精确匹配双分区结构,以规避相位调制干扰,选择了三个阶数间隔为二的轨道角动量模式作为输入。经过偏振控制,三个同轴入射模式为x|0⟩、x|2⟩和y|4⟩,位置A的模式场直径分别为1.8毫米、3.3毫米和4.4毫米。结合两个半波板和加载在空间光调制器上的分区恒定相位轮廓(1080×1080像素,像素间距为8.0微米),对这三个轨道角动量信道进行偏振变换,位置B的模式变为x|0⟩、y|−2⟩和x|−4⟩。随后,通过利用空间光调制器对三个轨道角动量模式施加分区螺旋相位调制,经过第一个半波板后观察到的位置C的模式为y|4⟩、x|2⟩和y|2⟩。最后,通过空间光调制器实现均匀螺旋相位调制,第二个半波板进行偏振转换,以及镜子的反射,位置D的输出轨道角动量模式变为x|4⟩、y|0⟩和x|2⟩。因此,实现了3个轨道角动量模式与两个偏振信道的交叉连接。值得指出的是,对于加载在空间光调制器上的分区相位,调整了相位中心和外围区域的范围布局,以确保中心区域(直径约2毫米)仅对|0⟩阶轨道角动量模式响应,而其余模式则作用于外围区域。每两个空间光调制器之间的传播距离约为38厘米。

图2 用于交叉连接三个依赖偏振的轨道角动量模式的实验装置。右侧依次呈现加载在空间光调制器上的相位轮廓,比例尺为2毫米。
图3展示了这3个轨道角动量模式在交叉变换前后的测量强度和偏振分布。为了确定偏振的切换,研究人员采用斯托克斯偏振测量法对每个轨道角动量信道的偏振状态进行了数值计算。为了确认模式的转换,输入和输出的轨道角动量模式的阶数通过利用圆柱透镜进行了有效测量。暗衍射条纹的数量指示模式的阶数,条纹的倾斜方向代表阶数符号。从这些结果可以得出结论,这些轨道角动量信道的三个模式和两个偏振成功进行了交叉变换且与理论预测一致(x|0⟩变为x|4⟩,x|2⟩变为y|0⟩,y|4⟩变为x|2⟩)。

图3 三个轨道角动量模式在交叉变换前后的测量强度模式、偏振分布和圆柱透镜检测结果。
为了定量评估轨道角动量模式与偏振交叉变换的性能,研究人员首先分别对三个输入和输出模式的偏振对比度进行了表征。测量过程涉及使用目标轨道角动量模式照射偏振分束器,从中根据透射光功率PT和反射光功率PR计算偏振对比度(ξ=|PT−PR|/(PT+PR))。如图4(a)所示,三个输出轨道角动量模式的偏振对比度均超过0.947,反映出有效的偏振控制。研究人员还测量了这三个轨道角动量模式在交叉变换前后的纯度。模式纯度η的计算公式为η=PG/PS,其中,PG是通过适当的Q波片降解输出轨道角动量模式生成的滤波高斯光束的光功率,PS指输出光束的总光功率。从图4(b)可以看出,输出模式纯度超过0.951,这表明有效的模式变换。此外,测得的模式插入损耗和偏振转换损耗分别低于3.42 dB和3.54 dB。
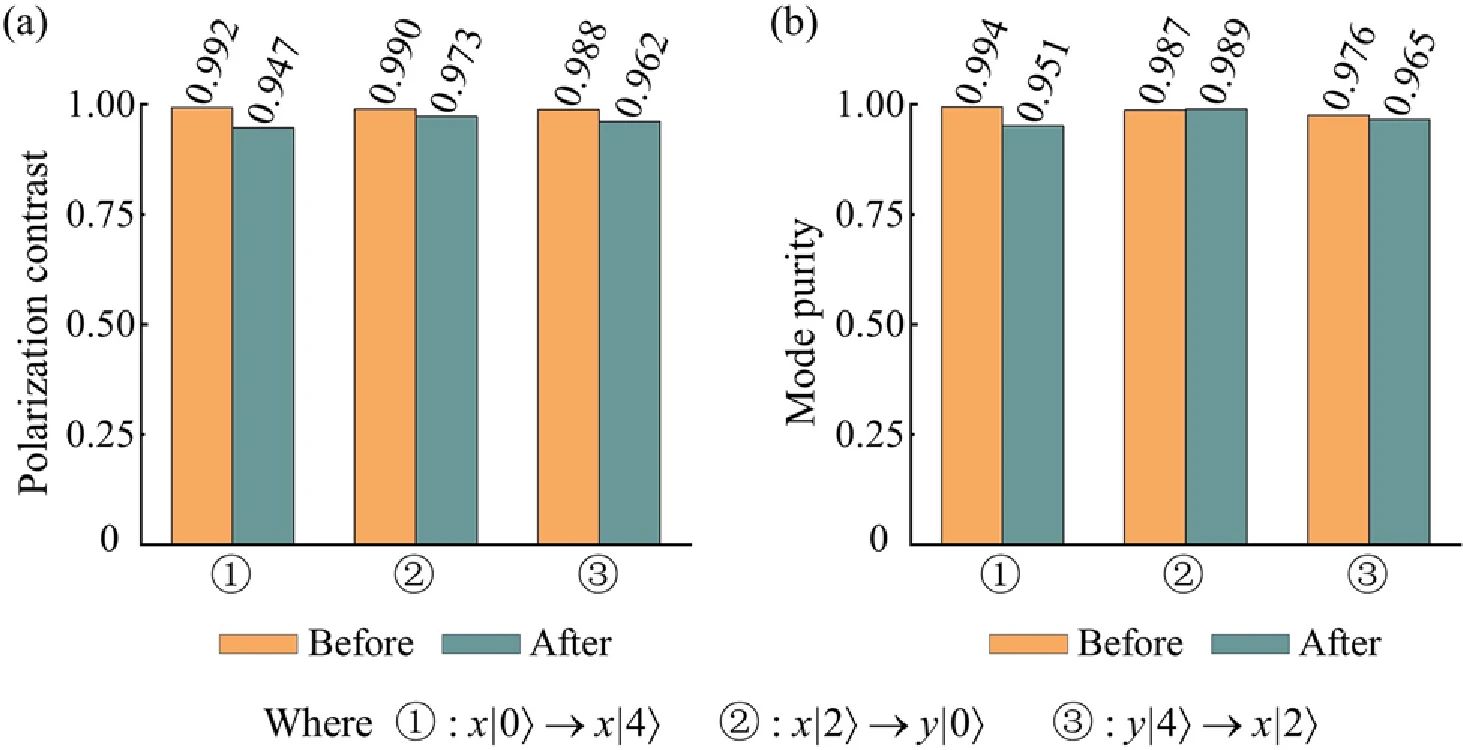
图4 轨道角动量模式与偏振交叉变换的定量表征,包括 (a) 偏振对比度和 (b) 模式纯度。
为了探索其应用潜力,研究人员构建了一个24信道依赖偏振的轨道角动量模式数据交换通信系统,结合了8个波长。通过同时进行波长分复用,每个3个复用模式信道(x|0⟩、x|2⟩和y|4⟩)承载400 Gb/s(=50 Gb/s×8)的相位调制信号进行交叉连接。这8个波长的光谱在交叉连接前后进行了实验测量,模式信道的串扰低于−24.6 dB。图5描绘了交叉连接前后3个轨道角动量模式信道捕获的时间波形。可以看出,这些信道的时间波形保持一致,显示了通过模式交叉连接成功实现信号交换。
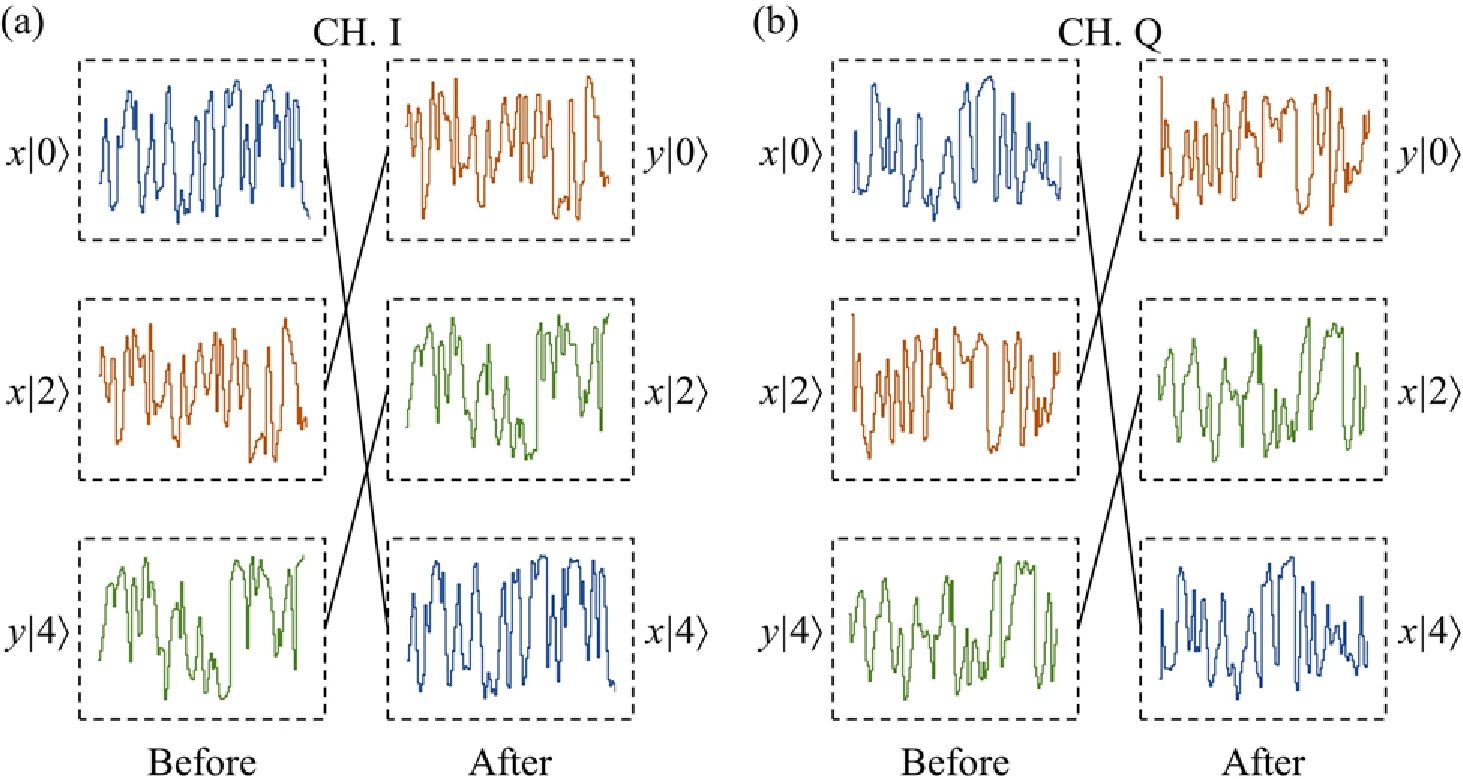
图5 三个模式信道在交叉连接前后观察到的解调波形,包括 (a) 同相分量和 (b) 正交分量。
此外,研究人员评估了轨道角动量模式信号在数据交换过程中的误码率性能。图6(a)展示了在波长1550.12 nm下,交叉连接前后模式信道x|0⟩、x|2⟩、y|4⟩和交叉连接后的模式信道x|4⟩、y|0⟩、x|2⟩的误码率曲线。在所有情况下,误码率均保持在3.8×10-3的硬判决前向错误纠正阈值以下且随着接收光功率的增加,所有信道的误码率接近10-6。图6(b)展示了接收光功率为−20.5 dBm时这些模式信道的星座图,显示出星座图中高度聚合的特征。图6(c)进一步展示了在接收光功率为−20 dBm时,交叉连接前后六个模式信道的误码率曲线,波长为1550.12 nm的星座图相似且聚合[图6(d)],这突显了良好的波长信道均衡性。通过星座分布计算得到的误差向量幅度低于20.74%。这些结果不仅表明通信系统具备良好的数据交换性能,还暗示所提出的轨道角动量模式与偏振交叉连接方案在光通信网络中展现出良好的前景。
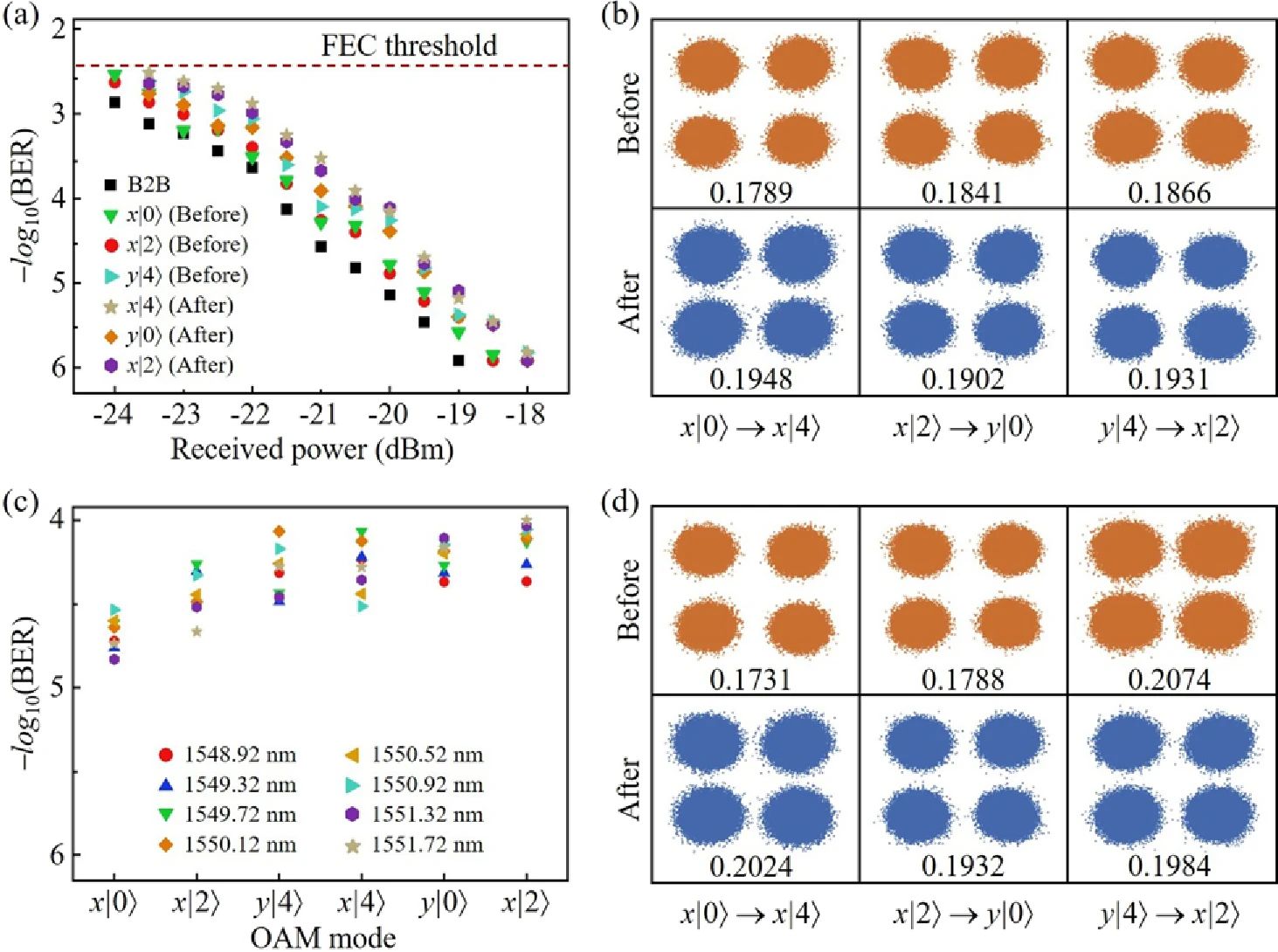
图6 使用轨道角动量模式交叉连接进行数据交换的通信结果。数据交换时模式信号的误码率曲线 (a) 在波长为1550.12 nm时和 (c) 在接收光功率为−20 dBm时。星座图 (b) 在−20.5 dBm时的 (a) 和 (d) 在1550.12 nm时的 (b)。
与以往方法相比,研究方案的优越性在于其在交叉连接过程中对每个模式信道的偏振控制灵活性,突破了以往固定输入输出偏振映射的限制。为了进一步证明这一点,研究人员通过重新建立轨道角动量信道的偏振状态映射关系,进行了保持偏振的轨道角动量模式交叉连接(x|0⟩转为y|4⟩、x|2⟩转为x|0⟩和y|4⟩转为x|2⟩)。所有比特错误率均低于接收光功率超过−23 dBm时的前向错误纠正阈值。此外,研究人员还展示了一个4信道依赖偏振的轨道角动量模式交叉连接(即x|0⟩转为y|1⟩、x|1⟩转为x|0⟩、y|2⟩转为y|3⟩和y|3⟩转为x|2⟩),通过适当建立输入输出模式和偏振的状态映射关系实现了4个模式和2个偏振的交叉变换。除了方法可通过增加分区相位调制来扩展交叉连接信道的数量外,对模式和偏振的全面控制显示出其在轨道角动量模式复用通信和网络中进行复杂多维信道处理的显著潜力。
总之,研究人员提出了一种轨道角动量模式与偏振交叉变换的解决方案,旨在实现模式与偏振复用信道的交叉连接,克服了传统交叉连接方法中存在的偏振转换限制。在分级分区相位调制的驱动下,分散分离的轨道角动量模式可以在不同的空间区域内独立进行模式和偏振处理,从而在实验中实现了三种模式和两种偏振复用信道的协同。基于这一理念,研究人员展示了1.2 Tbit/s四分相移键控信号的交叉连接。这项研究提出的策略在交叉连接轨道角动量模式偏振多维复用信道中的有效性,这在推动轨道角动量网络构建中的信道切换和光学节点互连的实际应用方面具有巨大潜力。
免责声明:本文旨在传递更多科研资讯及分享,所有其他媒、网来源均注明出处,如涉及版权问题,请作者第一时间联系我们,我们将协调进行处理,最终解释权归旭为光电所有。