用叉形光栅测量电子涡旋束的轨道角动量
专家视点
电子涡旋束,即电子以量子化轨道角动量在自由空间中传播现象,在被发现后,由于其独特的物理性质及其在新型电子显微镜和光谱学中的潜在应用,吸引了大量的关注。在此,Koh Saitoh等人通过实验研究了具有轨道角动量的电子涡旋束通过叉形光栅的衍射过程。通过Burgers矢量为1的叉形光栅后的n阶衍射电子涡旋束显示出n![]() 轨道角动量转移。因此,由于电子束之间的尺寸差异,衍射图案将镜像不对称。这种叉形光栅与位于衍射面上的针孔结合使用,可以作为分析仪来测量输入电子的轨道角动量。这项研究可能为电子显微镜的研究开辟新的途径,并为相关研究提供新的思路。该工作发表在Physical Review Letters上。
轨道角动量转移。因此,由于电子束之间的尺寸差异,衍射图案将镜像不对称。这种叉形光栅与位于衍射面上的针孔结合使用,可以作为分析仪来测量输入电子的轨道角动量。这项研究可能为电子显微镜的研究开辟新的途径,并为相关研究提供新的思路。该工作发表在Physical Review Letters上。

Koh Saitoh, Yuya Hasegawa, Kazuma Hirakawa, Nobuo Tanaka and Masaya Uchida. Measuring the orbital angular momentum of electron vortex beams using a forked grating, Physical Review Letters 111(7): 074801 (2013).
通过叉形光栅和螺旋带板形成一系列具有量子化轨道角动量的衍射电子涡旋束。实验中,研究人员将电子涡旋束注入叉形光栅中,观察输出光束的传播情况[图1(a)]。图1(b)和1(c)显示了研究的实验装置示意图。以厚度为50 nm的Si3N4膜为材料制备螺旋带板的二元掩模[图1(d)]和叉形光栅[图1(e)],利用聚焦离子束仪器(日立FB-2100)在膜的两侧分别沉积厚度约为100 nm的PtPd膜。在200 keV加速电压下工作的透射电子显微镜(JEOL JEM-2100F)聚光镜孔径位置分别插入螺旋带片和叉形光栅。衍射图由16位CCD摄像机用2k×2k像素,安装在Gatan成像滤光片的末端。由于其固有的高放大倍率,这种成像滤波器对观察图案的详细特征是有效的。
在聚光镜系统处插入拓扑荷为10的螺旋带片[图1(d)]。螺旋带区板产生一系列具有不同拓扑荷的电子涡旋束,沿传播方向聚焦于或发散于不同位置的点。由螺旋带板产生的n阶电子束的轨道角动量为10n![]() 通过改变聚光透镜系统的激发,可以调节电子涡旋束的会聚角。在叉形光栅上设置1阶或-1阶电子涡旋束,以满足平行照明条件。当1阶电子涡旋束满足平行照明条件时,一阶电子涡旋束不满足平行照明条件,反之亦然。在选定区域的孔径位置插入了一个Burgers矢量为1的叉状位错光栅[图1(e)]。
通过改变聚光透镜系统的激发,可以调节电子涡旋束的会聚角。在叉形光栅上设置1阶或-1阶电子涡旋束,以满足平行照明条件。当1阶电子涡旋束满足平行照明条件时,一阶电子涡旋束不满足平行照明条件,反之亦然。在选定区域的孔径位置插入了一个Burgers矢量为1的叉状位错光栅[图1(e)]。
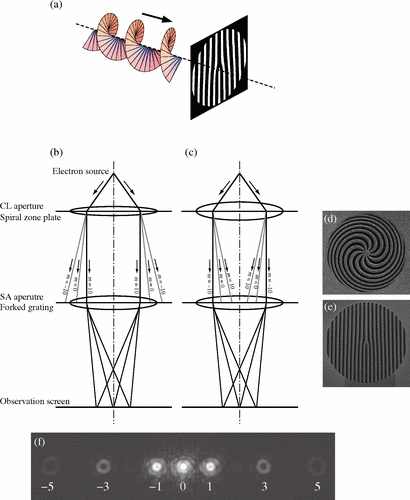
图1 (a) 实验示意图。(b)、(c) 实验装置的射线路径图。设置m=10 (b)和m=-10。 (c) 电子涡旋束满足平行光束条件,经分叉光栅衍射,在屏幕处形成衍射图案。(d) 在聚光镜孔径位置引入直径约为20 μm的螺旋带板。(e) 在选定区域的孔径位置引入直径约为30 μm的叉形光栅。(f) 由(e)所示的叉形光栅形成的衍射图样。
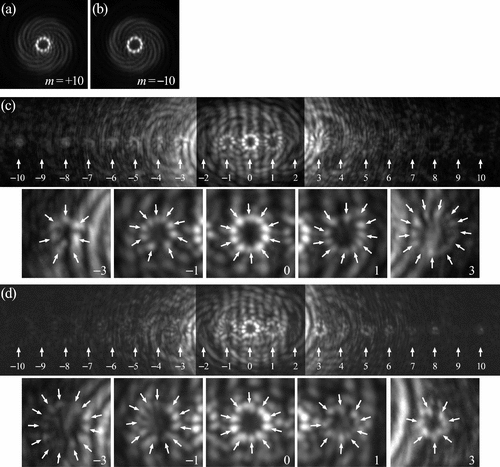
当叉形光栅与针孔结合使用时,可以传递电子轨道角动量,从而成为测量自由电子轨道角动量的有效工具。这种技术让人联想到光学中的单模光纤。假设一个轨道角动量为m![]() 的电子涡旋束入射到一个b=1的叉形光栅上,则m级衍射光束是一个具有尖峰的平面波,对应于电子轨道角动量转移m
的电子涡旋束入射到一个b=1的叉形光栅上,则m级衍射光束是一个具有尖峰的平面波,对应于电子轨道角动量转移m![]() 。此外,如果在衍射平面上第m个衍射峰的位置放置一个针孔,它只选择轨道角动量为零的电子对应的尖锐衍射峰。结合针孔的叉形光栅可以作为分析仪(分选器)来测量输入电子的轨道角动量。
。此外,如果在衍射平面上第m个衍射峰的位置放置一个针孔,它只选择轨道角动量为零的电子对应的尖锐衍射峰。结合针孔的叉形光栅可以作为分析仪(分选器)来测量输入电子的轨道角动量。
这种电子轨道角动量分析仪具有广泛的应用,尤其是在材料科学领域。在伴随原子内壳激发的特定非弹性散射过程中,散射的自由电子和被激发的原子电子之间的动量传递可以具有各向异性,反映了被激发原子电子的初始状态以及最终状态的各向异性。伴随着的Δl=±1的角动量转移,从初始态到最终态的激发被认为是一个很好的近似偶极子跃迁。因此,轨道角动量可以在原子电子跃迁的反冲过程中,通过非弹性散射转移到自由电子上。设置在试样后平面上的b=±1叉形光栅,可以通过观察1阶和-1阶衍射光束来区分具有![]() 或-
或-![]() 轨道角动量的非弹性散射电子。此外,可以使用针孔只选择零轨道角动量或其他特定轨道角动量的电子。由于磁自旋与激发的最终态相耦合,即自旋向上和自旋向下的态分别与Δl=+1和Δl=-1的跃迁有关,因此,可以利用叉形光栅测量非弹性散射电子的轨道角动量来探测磁自旋。此外,电子轨道角动量分析仪不仅可以应用于偶极相互作用,还可以应用于四极和高阶多极相互作用。
轨道角动量的非弹性散射电子。此外,可以使用针孔只选择零轨道角动量或其他特定轨道角动量的电子。由于磁自旋与激发的最终态相耦合,即自旋向上和自旋向下的态分别与Δl=+1和Δl=-1的跃迁有关,因此,可以利用叉形光栅测量非弹性散射电子的轨道角动量来探测磁自旋。此外,电子轨道角动量分析仪不仅可以应用于偶极相互作用,还可以应用于四极和高阶多极相互作用。
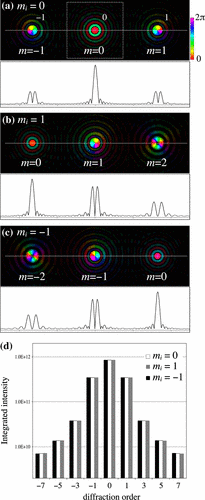
这项研究为理解Verbeeck等人观察到的二色性现象提供了重要线索。将叉形光栅贴在Fe薄膜后,研究人员观察到叉形光栅的1阶和-1阶衍射电子束在Fe-L23峰的电子能量损失谱信号有显著差异。如果离开Fe薄膜的非弹性散射电子在m=![]() 处形成涡旋束,则1阶和-1阶衍射束分别对应m=2
处形成涡旋束,则1阶和-1阶衍射束分别对应m=2![]() 和m=0;另一方面,如果离开Fe薄膜的非弹性散射电子形成m=-
和m=0;另一方面,如果离开Fe薄膜的非弹性散射电子形成m=-![]() 的涡旋束,则1阶和-1阶束分别对应m=0和2
的涡旋束,则1阶和-1阶束分别对应m=0和2![]() 。如图3所示,两种情况下的衍射图案都是镜面不对称的。然而,由于上述原因,电子能量损失谱信号中的二色性不能简单地通过比较整个1阶衍射束的总强度来解释,即使在Δl=+1和Δl=-1之间发生跃迁的概率存在差异。在电子能量损失谱实验中,选择“尖锐”衍射光束的中心部分可能需要考虑“针孔效应”。
。如图3所示,两种情况下的衍射图案都是镜面不对称的。然而,由于上述原因,电子能量损失谱信号中的二色性不能简单地通过比较整个1阶衍射束的总强度来解释,即使在Δl=+1和Δl=-1之间发生跃迁的概率存在差异。在电子能量损失谱实验中,选择“尖锐”衍射光束的中心部分可能需要考虑“针孔效应”。
总之,研究人员用叉形光栅研究了电子涡旋束的轨道角动量转移。由Burgers矢量为1的叉形光栅产生的n阶衍射电子涡旋束的轨道角动量转移为n![]() 。当这种叉形光栅与针孔结合使用时,可以用作电子轨道角动量分析仪。这项研究可能为电子显微镜的研究开辟新的途径,并为相关研究提供新的思路。这种方法不仅适用于磁性材料,也适用于非磁性材料。例如,在电子显微镜中测量二次电子的轨道角动量和在光电子能谱中测量光电子的轨道角动量是很有趣的。此外,它也可以应用于电场和磁场的测量,因为不均匀的电场和磁场会导致轨道角动量转移。
。当这种叉形光栅与针孔结合使用时,可以用作电子轨道角动量分析仪。这项研究可能为电子显微镜的研究开辟新的途径,并为相关研究提供新的思路。这种方法不仅适用于磁性材料,也适用于非磁性材料。例如,在电子显微镜中测量二次电子的轨道角动量和在光电子能谱中测量光电子的轨道角动量是很有趣的。此外,它也可以应用于电场和磁场的测量,因为不均匀的电场和磁场会导致轨道角动量转移。
免责声明:本文旨在传递更多科研资讯及分享,所有其他媒、网来源均注明出处,如涉及版权问题,请作者第一时间联系我们,我们将协调进行处理,最终解释权归旭为光电所有。