Menu 

Menu
  1. 首页
  2. 行业新闻
  3. 全变差正则化傅里叶叠层稀疏孔径成像（OLEN）

全变差正则化傅里叶叠层稀疏孔径成像（OLEN）

TVFP：全变差正则化傅里叶叠层稀疏孔径成像 

Resolution Enhancement of Long-range Imaging with Sparse Apertures

本期导读

在远距离光学成像中，镜头口径造成的衍射模糊是限制成像分辨率的主要原因。合成孔径（Synthetic Aperture）可以有效地扩展成像系统的口径，突破单孔径成像的带宽限制，获得高分辨率的图像。然而相位信息难以直接记录，为合成孔径带来困难。傅里叶叠层成像技术将相位恢复技术与孔径扫描过程相结合，为合成孔径成像提供了一种新方案。为了克服相位恢复问题的不适定性，傅里叶叠层成像需要高的孔径重叠率来保证算法收敛性。这种通过密集的孔径扫描的采集方式会导致采集时间长、计算量大，限制了傅里叶叠层成像的应用。
    来自清华大学的研究人员提出了一种采用稀疏孔径进行傅里叶叠层成像的方法，通过引入全变差正则化降低了收敛性对孔径重叠率的依赖。该方法可以利用孔径拼接实现大孔径成像，摆脱了密集孔径扫描的限制，允许多个独立成像系统同时采集图像，能够自动获取孔径的相位畸变，简化了成像配置并提高了采集效率。该研究于2022年4月发表在《Optics and Lasers in Engineering》。

Image

技术路线

根据傅里叶光学理论，相干光学成像系统的孔径决定了物体频谱采集范围，通过改变照明角度或者使孔径发生移动，可以得到频谱不同位置的子频谱对应的图像，将这些包含子频谱数据的图像进行计算拼接可恢复出完整的物体频谱信息。由于像感器只能记录强度信息而丢失了相位信息，需要通过强度图像及其在频谱面的位置关系来恢复相位。
    为了克服相位恢复问题解的不唯一性，傅里叶叠层成像技术还需要各个子频谱具有足够的孔径重叠率，以保证每个子频谱的相位收敛到一致的解。而采用稀疏孔径进行频谱采样，孔径间相位关联性较弱，给图像重建带来了困难。本文提出全变差正则化傅里叶叠层成像方法（TVFP），通过对物体施加梯度域稀疏的先验约束，从而降低算法收敛性对于孔径重叠率的依赖，在孔径重叠率很小甚至没有重叠的情况下，依然能恢复完整的物体频谱信息。TVFP用于远距离成像的示意图如图1所示。

全变差正则化傅里叶叠层稀疏孔径成像（OLEN）

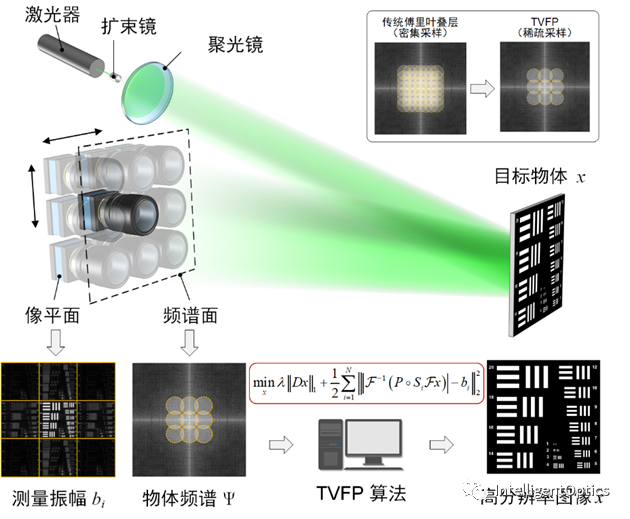
图 1 基于TVFP的稀疏孔径远距离成像示意图

图2展示了一组仿真实验，分别采用高斯牛顿法和TVFP方法对分辨率板进行重建。由于高斯牛顿法没有引入任何先验信息，仅能恢复出孔径采样区域内的频谱信息，且当采样孔径数量从7×7减少到3×3，对应的孔径重叠率从44%降低到25%时，重建图像的成像质量明显下降。通过比较合成孔径后等效点扩散函数（PSF）可以看出，稀疏的光谱采样导致了PSF严重的旁瓣效应。而TVFP方法在重建过程中施加了物体的先验信息，在3×3采样孔径情况下依然能恢复完整的频谱信息，重建出高分辨图像，其PSF接近理想成像系统的PSF。

 

全变差正则化傅里叶叠层稀疏孔径成像（OLEN）

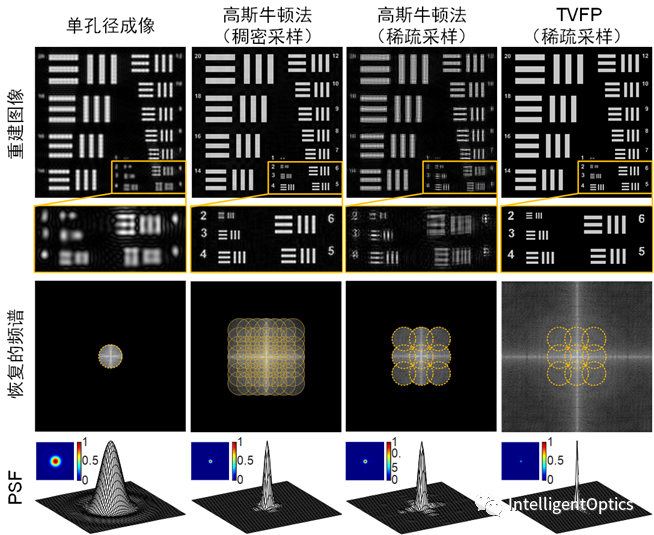
图 2 高斯牛顿法和TVFP方法重建分辨率板结果比较

 

在实际光学系统中，镜头像差的存在给傅里叶叠层成像模型带来了模型误差，影响图像的重建质量，而镜头的像差可以通过光瞳函数的相位畸变来表征。为此，本文在TVFP基础上提出光瞳函数和目标图像联合优化的eTVFP方法。通过交替优化目标图像和光瞳函数，实现光瞳函数的估计和高分辨图像的重建。图3给出了在光瞳函数存在相位畸变情况下TVFP和eTVFP对复振幅物体的重建结果。可以看到，由于存在相位畸变，TVFP方法并不能给出很好的重建结果。而eTVFP较为准确地估计出了光瞳函数的相位分布，并且清晰地重建出了振幅图像和相位图像。

Image

图 3 光瞳函数存在相位畸变情况下TVFP和eTVFP重建结果比较

 

图4展示了对分辨率板的成像实验。分辨率板放置在离成像系统1.5米远处，并通过会聚球面波照明。成像系统由透镜、光阑和像感器组成，其中光阑可以在垂直光轴平面内移动，用来模拟不同位置孔径的采集情况。首先采用7×7个采样孔径对分辨率板进行测量，其中孔径直径为2 mm，相邻孔径间距为1 mm。图4中给出了7×7张采集的强度图像和采用eTVFP方法重建的高分辨率振幅和相位图像，相当于用２ mm孔径镜头达到了8 mm孔径镜头的分辨率。

全变差正则化傅里叶叠层稀疏孔径成像（OLEN）

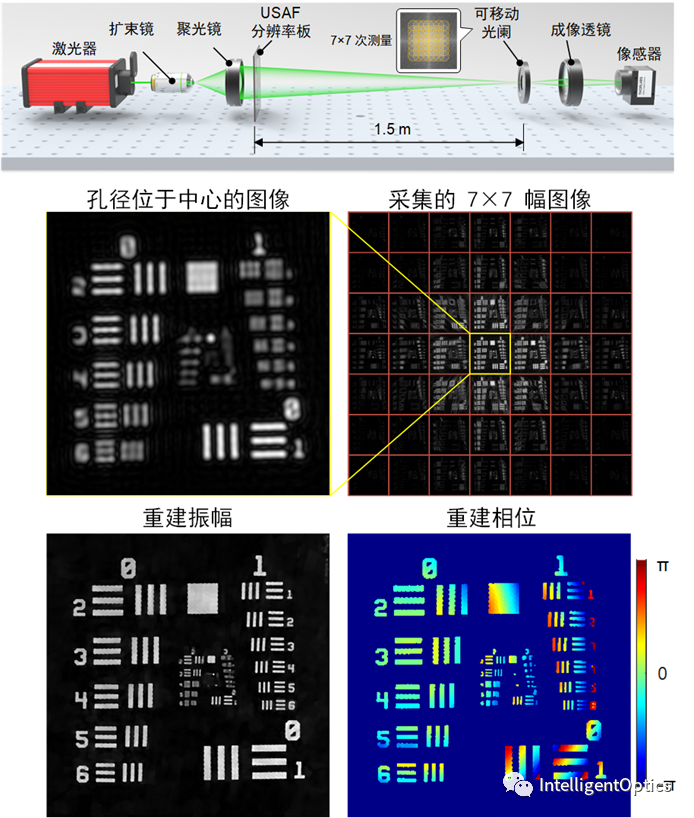
图 4 实验装置和eTVFP方法对分辨率板的重建结果

为进一步验证eTVFP方法对稀疏孔径采样下的图像重建能力，从49个测量图像中选择若干个图像进行重建，图5给出了孔径数量分别为49、17、9时高斯牛顿法和eTVFP方法的重建结果，所选图像的孔径在频谱中的位置以黄色圆圈突出显示。可以看到在稀疏孔径采样下，eTVFP方法重建质量优于高斯牛顿法，特别是在仅使用9幅图像的情况下，在边缘孔径与中心孔径没有频谱重叠的情况下，依然可以清晰重建图像的细节。

全变差正则化傅里叶叠层稀疏孔径成像（OLEN）

图 4 不同采样孔径数量下对分辨率板的重建结果

简单总结，该研究提出了一种基于全变差正则化的傅里叶叠层成像TVFP方法，可用于稀疏孔径的远距离成像。全变差正则化所施加的先验信息可以有效提高算法收敛性，减少冗余测量。进一步提出的eTVFP方法通过对目标物体和光瞳函数的联合优化，可以恢复光瞳函数的相位畸变。该研究展现了利用相机阵列代替孔径扫描实现远距离成像的潜力，有望实现对动态场景的观测。

论文信息：

  • Jiachen Wu, Feng Yang, and Liangcai Cao, "Resolution enhancement of long-range imaging with sparse apertures," Optics and Lasers in Engineering. 155, 107068 (2022).

技术详见:

https://authors.elsevier.com/a/1evuyWipggimu

程序下载:

https://github.com/THUHoloLab/TVFP

*该技术分享所涉及文字及图片源于作者论文和网络公开素材,不做任何商业用途。

本文注明来源为其他媒体或网站的文/图等稿件均为转载，如涉及版权等问题，请作者在20个工作日之内联系我们，我们将协调给予处理。最终解释权归旭为光电所有。

基于衍射图样分析的相位型空间光调制器标定（OLEN）基于衍射图样分析的相位型空间光调制器标定（OLEN） 高速三维测量，让稍纵不再即逝高速三维测量，让稍纵不再即逝 12张封面带你回顾Chinese Optics Letters的202212张封面带你回顾Chinese Optics Letters的2022 光学经典导读之一Ultrafast Lasers 第一章 色散介质中的平面波光学经典导读之一Ultrafast Lasers 第一章 色散介质中的平面波 Nat. Photonics|荧光显微的原位超分辨引擎Light杰青作者优秀论文展（8） Class5 白矮星 White Dwarf OPCPA powered by CoherentClass5 白矮星 White Dwarf OPCPA powered by Coherent 深度学习赋能下的光学计量：让“老司机”搭上“顺风车”深度学习赋能下的光学计量：让“老司机”搭上“顺风车”