基于波前编码和深度学习的低成本简易光学系统

论文题目Low-cost and simple optical system based on wavefront coding and deep learning下载地址https://opg.optica.org/ao/viewmedia.cfm?uri=ao-62-23-6171&seq=0

随着计算成像技术的发展，光学系统设计与数字算法的结合使得更多的成像任务更容易实现。波前编码（WFC）是一种典型的计算成像技术，用于解决光学孔径和景深的限制。在本文中，我们展示了一种基于WFC和深度学习的低成本且简单的光学系统。构建了一种在深度学习框架下针对相位板的优化编码方法，降低了对全视场像差校正的要求。光学编码仅通过双合透镜和一个简单的立方相位掩模实现，数字解码则使用深度残差UNet++网络框架。最终获得的图像具有良好的分辨率，而系统的景深扩大了13倍，这对于机器视觉中小零件的高精度检测和贴装具有重要意义。

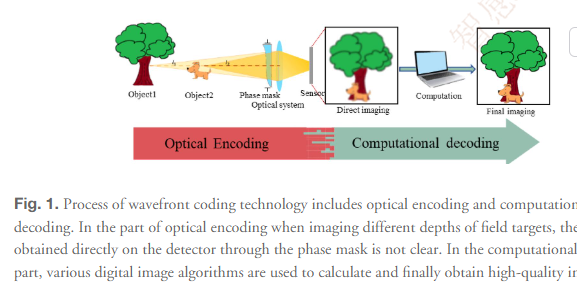
波前编码（WFC）是一种将光学系统与计算处理相结合的计算成像技术，近年来因其低成本、小尺寸和扩展的景深而备受关注。该技术最早由Dowski和Cathey于1995年提出，他们在孔径中放置了一个立方相位掩模。与传统光学系统设计相比，WFC系统包含一个相移掩模，确保光线不会集中在理想焦平面上的单个点。它在更宽的离焦范围内保持一致的光学传递函数。通过利用数字解码算法，根据光学系统编码信息重建图像，WFC技术扩展了光学系统的景深。由于其高光通量、分辨率和扩展的景深，WFC技术已在包括红外成像、显微镜和设计在内的各个领域得到了广泛的研究和应用。

为了获得更高质量和大景深的成像结果，研究主要集中在WFC成像链的两个方面：相位板编码的设计和解码算法的开发。自Dowski以来，已经引入了许多新的和复杂的相位掩模形式，包括对数相位掩模、指数相位掩模、微分相位掩模和正切相位掩模。掩模板的优化方法利用稳定相位法或菲涅尔积分法。解码部分的本质是基于光学系统的先验编码信息实现图像的去模糊。传统的解码算法，如维纳滤波或Lucy–Richardson去模糊算法，可能会在成像过程中引起振铃效应。近年来，随着深度学习的快速发展，许多方法将深度学习与WFC相结合，例如Du等人比较了生成对抗网络（GANs）和光纤通道网络交换机（FCNs）在使用神经网络对WFC成像系统进行高质量重建时的性能。Li等人将DeblurGAN与波前编码相结合，以实现红外光学系统中的大景深成像，Akpinar等人以端到端的方式使用神经网络设计了一个WFC系统。新的深度学习框架进一步增强了WFC技术的成像效果。

现代光学设计的发展对更小、更灵活、更轻的光学系统提出了需求。本文提出了一种高质量且简单的WFC系统，该系统仅包括一个相位掩模和一个双合透镜。由于高阶相位板的制造方法（包括自由曲面），因此其使用受到限制。因此，立方掩模仍然是WFC最常用的模板。为了在基于成像模型中成像的非线性退化的光学系统中保留部分像差，设计了一种基于不同视场下点扩散函数（PSF）差异的相位板优化方法。使用深度残差UNet (ResUnet)++ 来同时校正不同视场下的像差和编码效应。在简单的编码系统中，将景深从27.5毫米扩展到317.5毫米，扩大了13倍。该实验充分证明了优化的编码系统能够在简单的系统中捕获具有大景深的高质量图像，并促进了轻量化和小型化计算光学系统的研究。

2理论模型与设计方法

传统的波前编码技术包括两个步骤：光学编码和计算解码。在成像过程中，当成像系统捕获不同深度的目标信息时，会发生离焦模糊，导致直接成像模糊。通过使用数字算法，可以获得如图1所示的高质量恢复图像。如果在成像过程中存在聚焦误差，则实际光斑无法聚焦在探测器平面上。瞳孔相位函数表示为

其中φa是实际的瞳孔相位函数，da是点目标的共轭像点距离，x和y是透镜单元中的x和y坐标。相位差表示为

其中Wa是实际瞳孔相位与理想瞳孔相位之间的光程差，φi是理想瞳孔相位函数，di是探测器平面与瞳孔之间的距离。为了验证该方法的普遍性，设计了一个基本的三次相位掩模作为编码器，一个胶合消色差双透镜作为光学系统，并确定了探测器的位置。胶合消色差双透镜仅包含一个光学元件，并且具有系统复杂性低和用作光学系统时能量损失低的特点。尽管这种简单的光学系统消除了色差，但成像效果并不完美，仍然存在像差。三次相位掩模的功能表示为

其中α是如上所述的立方相位掩模参数，孔径函数表示成像系统出射光瞳中的振幅和相位分布。因此，通过在出射光瞳处添加编码图案，系统的PSF可以通过一些预先设计的图案来操纵。孔径函数可以表示为

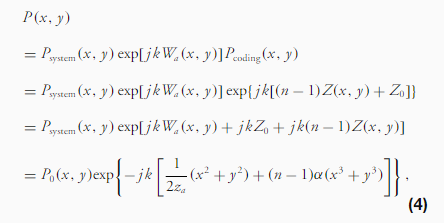
其中，P是编码孔径光瞳，Psystem是光学系统的聚焦光瞳函数，Pcoding是编码孔径光瞳函数，P0是光瞳函数中的不变部分，Z0是编码系统的最大厚度。因此，光瞳函数随离焦和编码特征参数而变化。PSF可以表示为

其中，符号 F {} 是傅里叶变换。此时，光学系统的 PSF 随离焦量、相位板特性参数和不同视场角而变化。如图 2 所示，在光学编码之前，模拟的 PSF 随不同视角下的离焦距离而急剧变化。当相机直接成像时，会发生图像退化，无法获得清晰的图像。

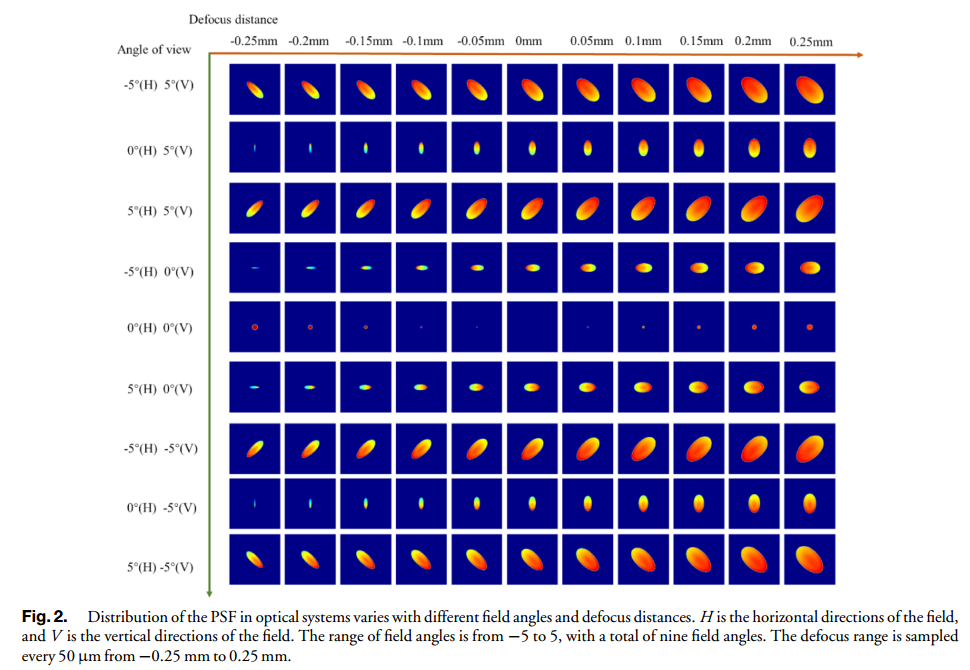
传统编码成像通常需要优化光学系统的所有视场成像质量，以实现每个视场的最高（MTF）质量。在这种情况下，PSF受到散焦和编码参数的影响。当检测到小视场和散焦范围时，光学系统可以表示为线性卷积模型

其中Iin是光学系统中的强度输入，Iout是光学系统中的强度输出，符号∗是卷积。考虑到基于图像特征的深度学习算法的工作特性，根据数据驱动模型对光学系统的成像过程进行反向拟合，并通过非线性退化模型实现不同视场的变化，从而实现图像校正。此时只需要要求对于同一视场，不同离焦水平的PSF相似即可。为了满足各种等距区域中PSF的离焦不变性，并考虑到编码图像的可恢复性，Zemax OpticStudio中的评价函数（MF）设置为

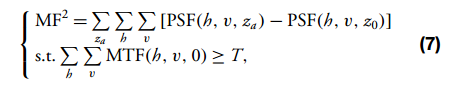
其中，向量“h”和“v”分别代表场分量的水平和垂直方向，MTF曲线的体积反映了PSF的中心能量。当给定参数“T”满足时，MTF曲线的体积限制了图像模糊的程度，为后续的解码计算提供更多信息。在实现中，T 被设置为 0.3。

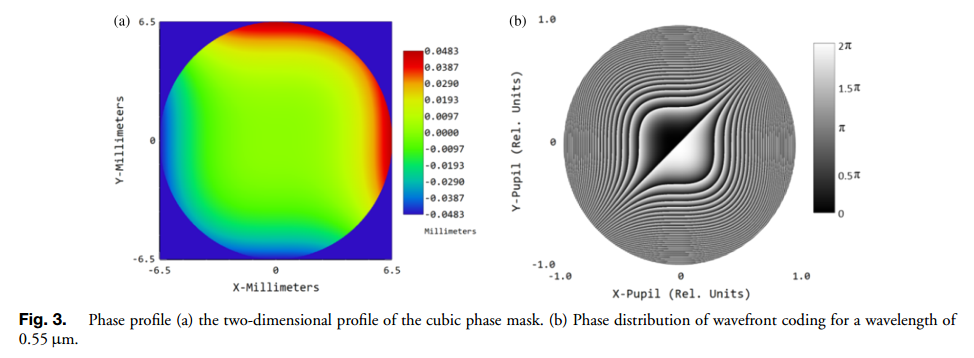
优化后，所设计系统的参数如表1所示。胶合消色差双透镜参数如下：F # = 4.5，EFFL = 50 mm，当立方相位掩模使用聚甲基丙烯酸甲酯时，相应的表面参数为0.000176。相位掩模轮廓如图3(a)所示，编码光瞳在波长0.55 μm处的波前相位如图3(b)所示。计算景深的经验公式表示如下：

当像距为 52 ± 0.022 mm 时，景深 (DOF) 为 27.5033 mm。同样地，当像距为 52 ± 0.25 mm 时，景深为 317.46 mm，景深扩大了 13.1083 倍。

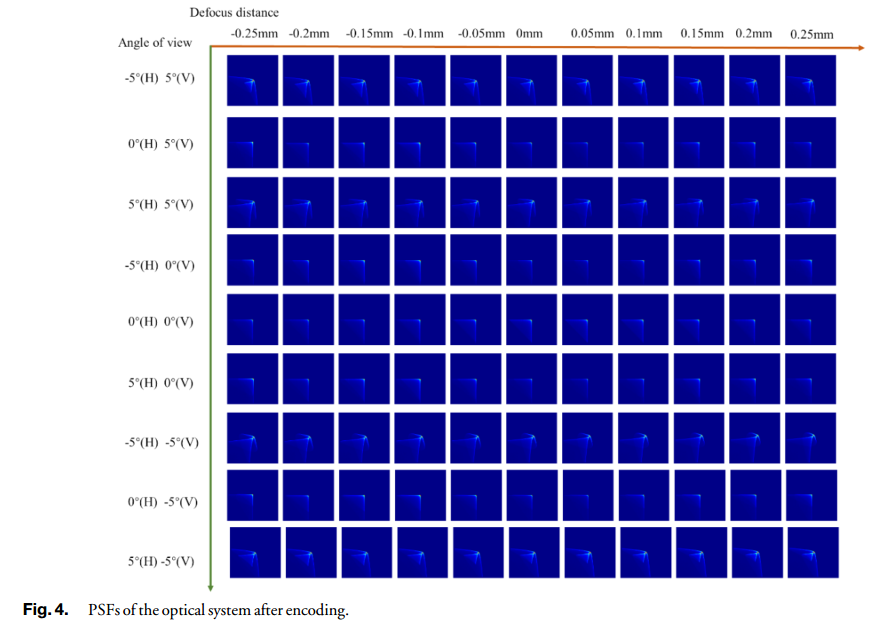
如图4所示，研究了观测平面上的PSF。离焦距离从−0.25 mm变化到0.25 mm，并且PSF在每个水平和垂直视角中都表现出高度的一致性。这种一致性作为后续章节中描述的数字解码过程的先验。

3. 数字解码算法

本文利用ResUNet++作为数字解码算法，ResUNet++架构与ResUNet模型有一些相似之处，但结合了额外的特征，例如挤压和激励块、空洞空间金字塔池化块和注意力块，如图5所示

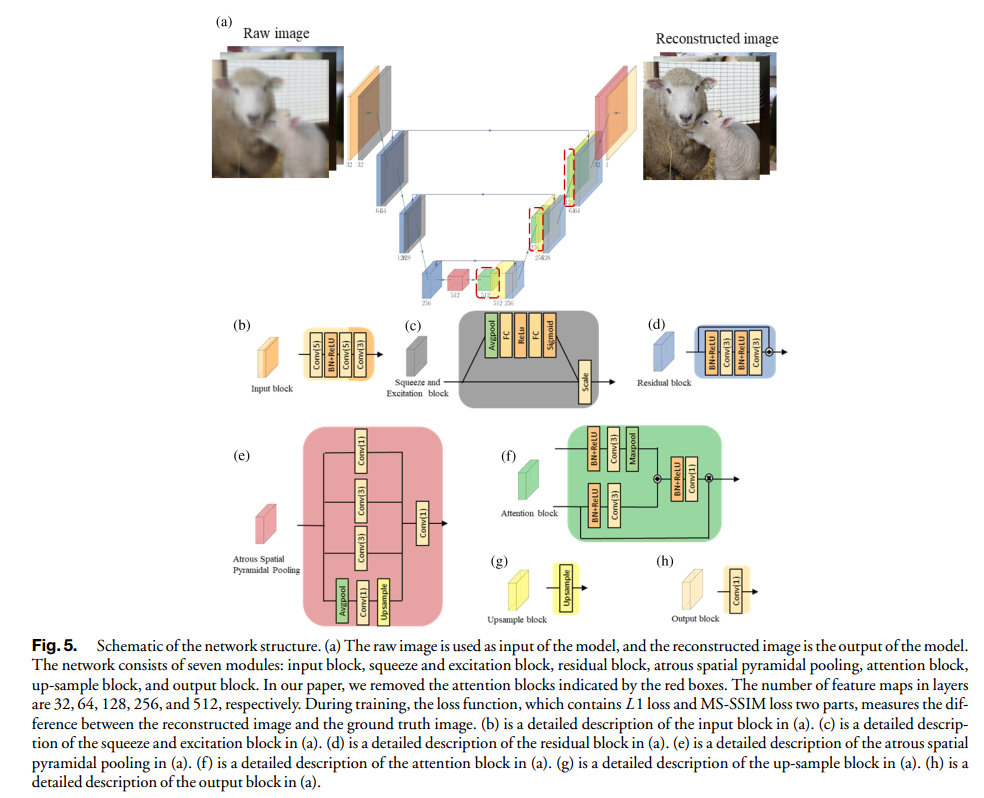
对实现进行了修改，注意力机制起源于医学图像检测，它增强图像中感兴趣的区域并抑制不相关的背景区域。由于 WFC 系统会降低图像的整个视野，并且退化模式取决于不同像素位置的 PSF，因此从系统中移除了注意力模块

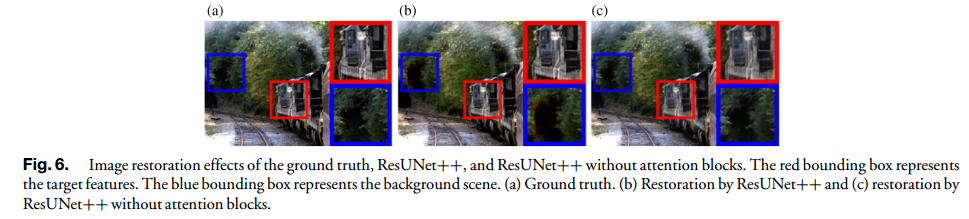
ResUNet++ 架构。在图 6 中展示了算法在使用和不使用注意力模块时的结果。图中红色框表示目标货运列车对象，而蓝色框表示具有黑色和树木纹理的背景区域。在图 6(b) 中，使用注意力块的修复结果显示相似性指数 (SSIM) 为 0.8146，峰值信噪比 (PSNR) 为 25.9284。目标区域的修复性能良好，SSIM 为 0.8146，PSNR 为 25.9284。然而，背景区域存在颜色失真，SSIM 为 0.8969，PSNR 为 24.2134。在移除图 6(c) 中的注意力块后，整体 SSIM 为 0.8859，PSNR 为 27.1015。目标区域的 SSIM 为 0.9497，PSNR 为 30.9784，低于使用注意力块的结果。然而，背景区域的 SSIM 也为 0.8890，PSNR 为 31.1644，优于使用注意力块的结果。通过移除注意力块，图 6(c) 中恢复的图像呈现出更清晰的整体结构，使其更适合我们的论文。此外，基于光学系统的 PSF 大小，改变了编码器块的配置方式为：输入块使用 5 × 5 的卷积块，以提供不同的感受野，而不是使用两个连续的 3 × 3 卷积核。

在论文中使用的损失函数是两个误差函数的组合，即L1正则化和平均结构相似性指标（MS-SSIM）。L1正则化衡量的是重建图像R和真实图像G之间的欧几里得距离，这可以提高鲁棒性。另一方面，MS-SSIM衡量的是两幅图像之间的结构相似性，有助于恢复更高质量的图像。通过结合L1正则化和MS-SSIM的优点，我们的模型能够有效地学习编码图像和相应的清晰图像之间的映射。损失函数可以表示为

其中β是一个超参数，用于控制两个误差函数之间的平衡。g代表真实图像，rˆ代表重建图像，G代表边缘像素和中心像素之间的高斯权重。在实验中，我们将β设置为0.7，这已被发现对WFC系统有效。由于WFC系统中的PSF与高斯噪声无关，因此高斯加权损失函数中的权重因子G可以设置为1。这意味着损失函数仅考虑真实图像和重建图像之间的差异，而没有给边缘额外的权重。

ResUNet++模型是使用VS code框架和PyTorch后端（Python版本= 3.8.5）实现的，并在配备Intel Core i7-9700 CPU和NVIDIA RTX 2060 GPU的工作站上进行训练。我们使用了Adam优化器，初始学习率为10⁻³。在训练过程中，当损失函数变化缓慢时，学习率乘以0.5，直到学习率降至10⁻⁸。

4. 仿真与分析

为了在使用ResUNet++模型进行数字解码时获得更准确的结果，需要足够的训练数据，并且数据集必须尽可能地接近实际场景。生成数据的模拟设置如图7所示。所提供的数据集包含11个模拟PSF，其离焦距离范围从−0.25 mm到0.25 mm。每个PSF包含红色、绿色和蓝色（RGB）通道波长的8个×8空间变化的PSF。基于不同空间位置上相应波长的PSF，根据公式(6)对三通道RGB图像进行降质和模拟。使用加性高斯白噪声方法设置了模拟的10 dB噪声水平。训练集、验证集和测试数据集是基于具有原始数据集的光学编码参数生成的。对于原始数据集，选择了两个公开可用的数据集，即随机选择了2000张图像的PASCAL VOC2012和随机选择了5000张清晰图像的PatternNet。总共为该数据集生成了7000个样本，包括一个包含5000个样本的训练集，一个包含1000个样本的验证集和一个包含1000个样本的测试集。

在网络训练之后，通过与维纳滤波、LR 、FCN-8s、DeblurGAN和 UNet 方法 进行比较来评估我们方法的性能。传统的算法依赖于先验模糊核进行逆滤波，而深度学习算法则使用模型来拟合非线性成像过程。图 8 中展示了一组比较结果，清楚地表明深度学习算法重建的图像比非深度学习算法重建的图像好得多。传统算法需要稳定的 PSF 进行逆滤波，这在简单的 WFC 系统中不能很好地应用。另一方面，FCN-8s 网络无法实现像素级别的恢复，并且常常无法保留精细的图像细节。相比之下，DeblurGAN、UNet 和我们的论文展示了更优越的恢复效果。我们的算法取得了显著的成果，在数据集上的平均 PSNR 值为 30.4934，平均 SSIM 值为 0.9347。

在我们的论文中，使用了一个包含各种离焦距离下的退化图像的数据集。ResUNet++网络经过训练，可以使用物理模型学习光学成像的逆过程。通过将此物理模型纳入训练过程，旨在增强ResUNet++模型准确恢复退化图像的能力。这种方法能够超越传统的图像处理技术，并利用底层物理学的知识来提高恢复性能。此外，ResUNet++模型的U型编码器-解码器架构结合了跳跃连接。这些连接使得在升采样阶段能够融合深层特征和浅层特征。通过这样做，该模型保留了局部信息，并防止了在图像恢复过程中重要细节的丢失。这种设计选择增强了图像重建的有效性，并有助于ResUNet++模型的整体性能。这些比较表明，ResUNet++模型对于解决数字解码任务是稳健的。

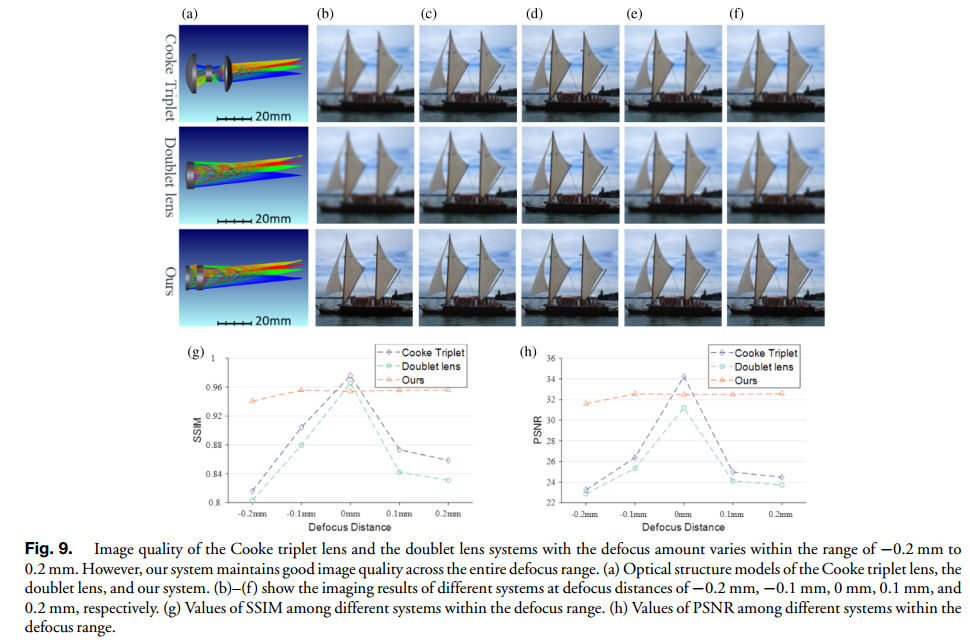
还在相同的光学焦距、F数和视场条件下比较了库克三片式透镜、双合透镜和我们系统的性能。图9(a)展示了这三个系统的光学模型。库克三片式透镜，从第一个透镜元件到像面，体积为22.946 cm3，质量为13.509 g。双合透镜的体积为15.053 cm3，质量为1.569 g。我们的WFC系统的体积为15.053 cm3，质量为1.860 g。模拟了这三个系统在−0.2 mm到+0.2 mm的离焦距离下的成像性能。库克三片式透镜在焦内位置表现出优异的成像性能，而随着离焦距离的增加，其图像质量会下降。类似地，双合透镜也显示出图像质量随着离焦距离的增加而下降。相比之下，我们的系统以其紧凑的尺寸和低质量为特征，在更大的离焦范围内表现出稳定和高质量的成像性能。

5. 结论

本文研究了WFC在简单光学系统中的性能。在该光学系统中，光学像差由系统的配置决定。这些像差与编码掩模一起形成了一种光学编码组合，可以进行数字解码，从而降低了传统光学系统的复杂性。成像结果使用残差神经网络进行解码，结果表明，与传统的复原方法相比，解码后的图像包含更精细的结构信息，具有不明显的振铃伪影和更好的成像质量。未来的研究将涉及基于该算法制造一个实际系统，以实现具有大景深、宽视场以及低尺寸和重量的高质量成像。本文验证了简单编码系统的深度扩展能力，促进了轻量化和便捷计算光学系统的发展，并为WFC技术在无人机、医学成像和低成本工业检测等领域的应用开辟了可能性。