计量学的新突破：利用涡旋光进行探测与传感

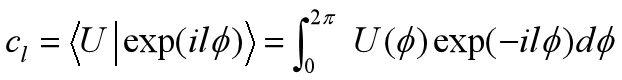
模态分解法通过正交基模式解析复杂光场，在光通信领域为高效信息编码与传输提供支撑，同时在需要精确光场表征的光学计量与成像技术中发挥关键作用。

 

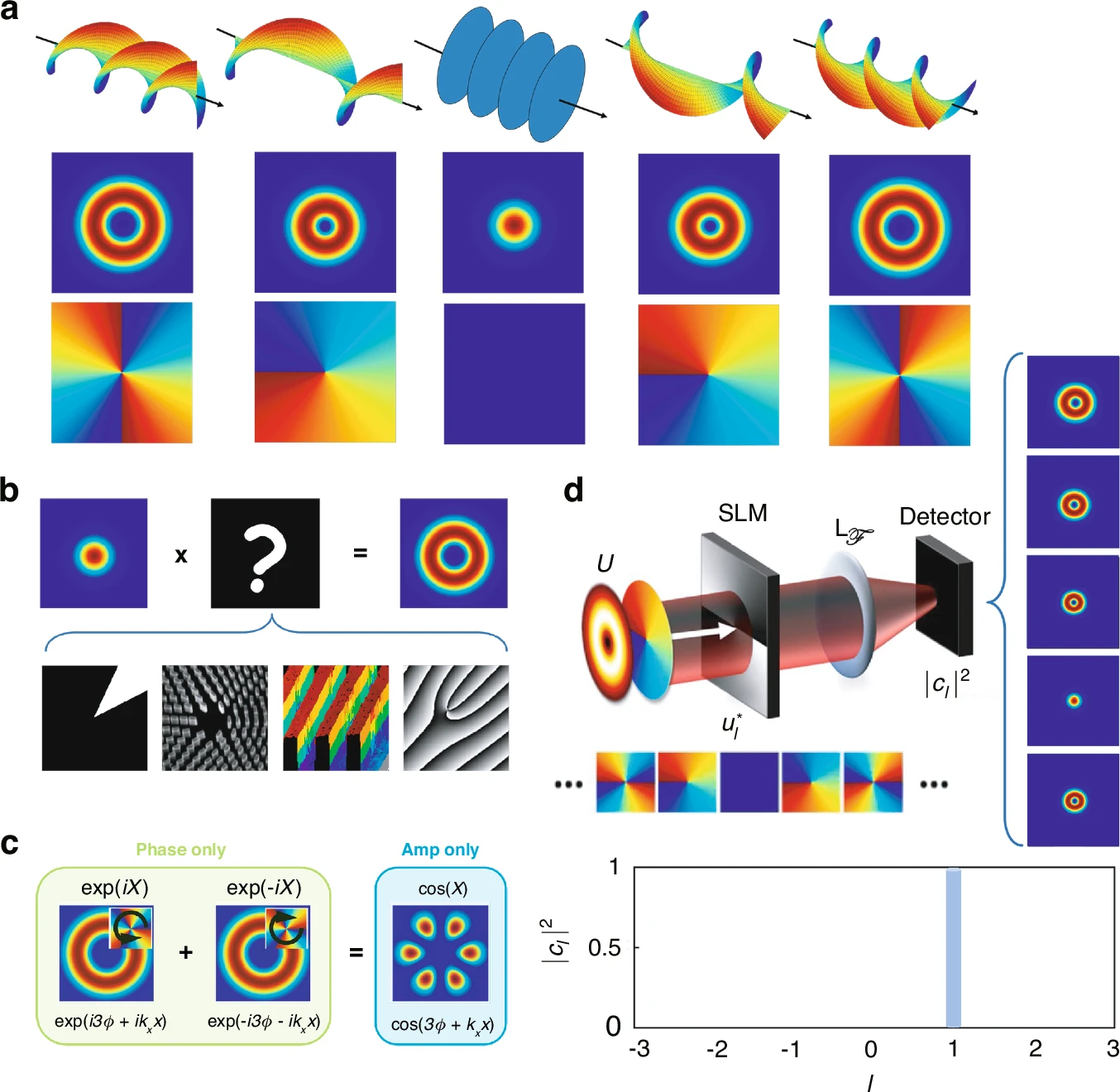
图1 涡旋光束的生成与检测。（a）轨道角动量光束特性（图示拓扑荷值从0至±2，符号决定相位变化方向）。（b） 轨道角动量光束调控技术，从左至右：扇形振幅掩模、超表面相位调控、衍射光学元件和叉形光栅数字全息。（c）相位-振幅转换原理。（d）轨道角动量模态分解检测。

轨道角动量谱测量的典型实验方案如下：光场U经调制，随后由傅里叶透镜L_{F进行傅里叶变换。可证明傅里叶空间中的轴上光强是成比例的，由此提取归一化模态分布，其特性类似于频谱。其他检测手段包括基于共形映射与干涉原理的确定性轨道角动量模式分选方法。}

_{涡旋光束的兴起推动了光通信、显微成像、微操纵等领域的创新突破。在光通信中，其独特的轨道角动量态革新了调制、编码与复用技术，显著提升数据传输安全性；在光学显微领域，涡旋光与物质的相互作用实现了超越传统显微技术的超高精度形貌分析与定量表征。}

_{传统光学计量依赖两列平面波干涉产生的线性相位梯度，虽具基础性但存在局限。通过拓展光的物理属性维度并开发创新技术，相关研究取得了重大突破。其中，涡旋光束的引入标志着计量学的范式革新——其独特的相位结构与轨道角动量特性，相较传统光源显著提升测量精度与分辨率，不仅增强了基础测量能力，更将光学计量的应用潜力推向新高度。}

_{涡旋光束的核心优势在于通过线性与旋转多普勒效应，实现对运动目标三维运动的同步测量。这一突破性能力深刻影响了微纳工程、生物医学、深空探测、精密监控、量子传感及环境监测等需极致精度与深度解析的领域。图2通过整合光的附加属性（或自由度）阐明了光学计量的重要发展方向：从单维光强属性应用，到光强与另一物理属性结合的二维测量，再到光强与双附加属性协同的三维探测，最终通过全维度物理属性的综合利用，实现测量精度、准确性、全面性与灵敏度的跨越式提升。}

_{从理论构想发展为现代光学核心要素的涡旋光束，在光学处理与操控技术进步驱动下，展现出巨大的应用潜能。其多维物理属性开发能力远超其他光束类型，催生了系列突破性发现与创新应用。研究人员通过典型案例研究，系统论证涡旋光在计量学中的独特价值：实现高精度测量、突破分辨率极限、拓展传统技术边界，最终揭示涡旋光复杂结构所承载的丰富信息维度，为计量学发展提供全新范式。}

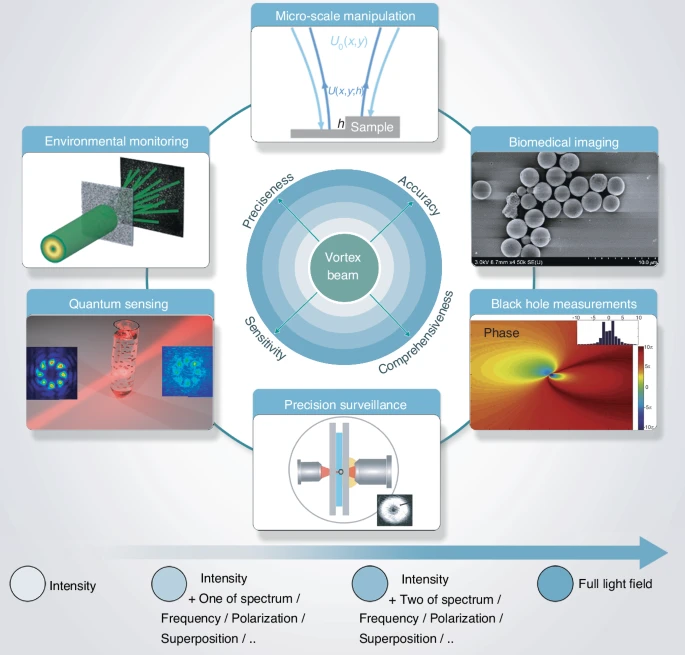
图2 光学计量学演进。图片展示了光学计量从单一光强参数应用向多维物理属性综合开发的演进过程，最终实现光场数据的全域化利用。

01

基于旋转多普勒效应的涡旋光动力学检测

传统光测动力学方法依赖多普勒效应，通过频率偏移测量物体或流体速度。然而，标准线性多普勒效应仅能探测目标相对于观测者的径向运动，无法检测横向与旋转运动。为突破这一局限，需深入挖掘光场的空间结构特性。标量涡旋光束的坡印廷矢量在光束横截面各位置具有方位角分量，表征光动量绕轴环流的特性。探测光束的方位角相位结构在与观测者或被照物体的旋转动力学相互作用时，可提取目标位置与速度信息，引发与横向位变相关的频移，即旋转多普勒效应。由于涡旋光束相位方位角变化速率为每圈 l×2π ，其与旋转运动耦合产生的频移正比于旋转角速度与轨道角动量模式数。因此，涡旋光束经旋转物体散射或反射后，产生的旋转多普勒频移可达圆偏振光束的数倍，理论与实验均验证了其测量旋转速度的有效性。

涡旋光束通过引入螺旋相位要素，显著拓展了多普勒计量能力（尤其当结合叠加态、双频、时间、偏振、空间结构及阵列配置等多自由度时，如图3所示）。与传统线性多普勒效应不同，旋转多普勒效应保持入射光束轨道角动量不变。当叠加态轨道角动量模式（l1与l2）与旋转物体相互作用时，频移放大效应与 |l1-l2| 成正比。旋转多普勒效应检测依赖内部关联的轨道角动量谱（而非单模相干性），使其可适用于非相干光源。采用双频涡旋光束作为探针，可将多普勒信号从低频域转换至高频域，有效抑制噪声并增强旋转方向分辨能力。时频分析技术动态监测角速度时序变化，实现旋转运动状态评估。千米级空芯光纤测速仪通过偏振与轨道角动量的矢量旋转多普勒效应融合，可解析矢量角速度；利用反向偏振涡旋光束干涉实现微小目标速度-方向同步检测，并通过非均匀偏振模式提升运动感知精度。探索探测光束的空间结构特性（如利用拉盖尔-高斯光束的径向-角向模式）可优化复杂径向结构目标的旋转多普勒效应检测效能。叠加光学涡旋阵列的全域轨道角动量模态聚集效应，则能增强信号幅度并提升非共轴入射鲁棒性。

 

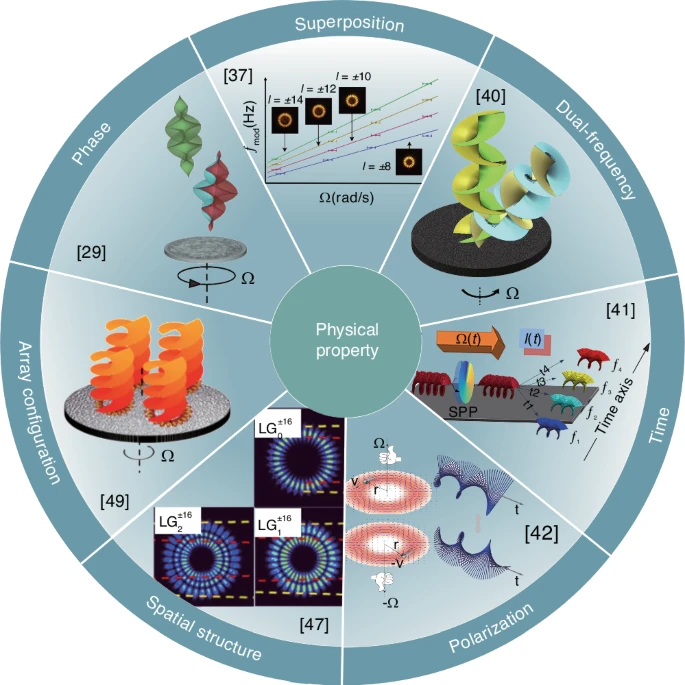
图3 基于轨道角动量的多普勒计量学。通过融合涡旋光束螺旋相位特性与多维度调控策略（包括叠加态、双频、时间、偏振、空间结构及阵列配置），革新多普勒计量技术，实现信号幅度增强、测量精度提升与系统鲁棒性优化，同步支持旋转方向判定与加速度分析。

基于涡旋光旋转多普勒效应的光学计量技术已从二维动力学评估演进至三维综合检测，如图4所示。该技术最初聚焦旋转速度测量，现已扩展至旋转方向判定、加速度测量、几何对称性分析及转轴定位等领域。例如，利用拉盖尔-高斯光束照明可解析三维螺旋轨迹粒子的平动与旋转速度分量：粒子旋转与纵向运动引发的特征频移差异可实现运动方向判定——当探针相位旋转方向与粒子旋转方向一致时频偏最小，反之则频偏最大。动态结构光引发的频变特性为运动方向解析提供新途径，亦可通过双频涡旋探针或反向偏振涡旋光束干涉实现旋转方向判别。

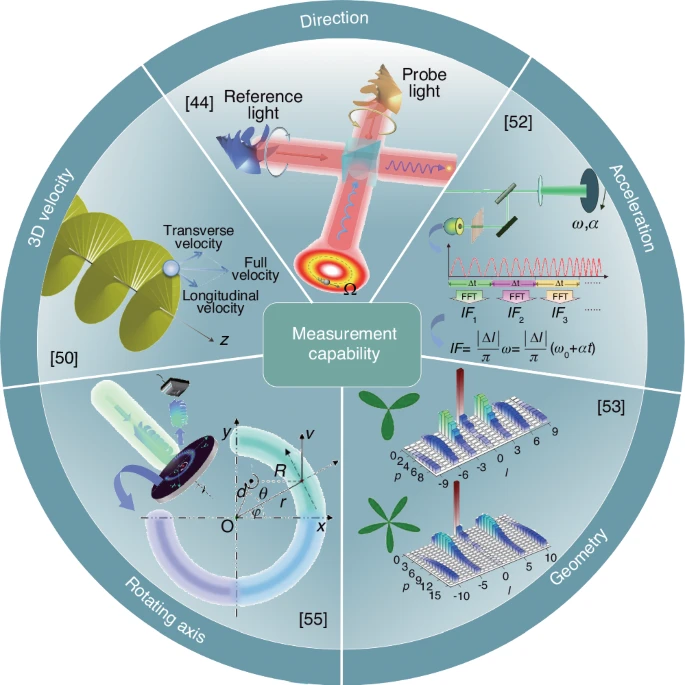
图4  多普勒计量学进展。多普勒计量技术已从二维旋转速度评估演进至三维速度综合检测，涵盖旋转方向判定、加速度测定、几何对称性分析及转轴定位。

融合轨道角动量调制的时频分析技术可同步评估旋转速度与加速度，在维持系统简洁性的同时提升测量精度。旋转多普勒频移诊断技术不仅实现远距离旋转速度与几何对称性分析，更通过倍频上转换探测将旋转多普勒效应扩展至红外波段。具有非对称缺陷的拼接叠加涡旋对物体转轴高度敏感，作为探针光束可快速确定转轴方位，为旋转表面轴系校准提供关键支持。

理论与实验研究显著推进了旋转多普勒效应计量学发展，使其从理想入射条件拓展至微物体旋转检测、微小转角、斜入射及横向偏移等复杂场景，如图5所示。探测器处两异模轨道角动量叠加干涉可放大观测多普勒频移，实现微生物运动特性精细解析。通过被测与参考涡旋光束共轴干涉产生的干涉瓣旋转角/向监测，可探测微位移与运动方向。参考光路与测量光路采用反向轨道角动量涡旋光束干涉时，花瓣状光斑旋转可表征速度微小变化，其转速与时变相位差直接相关。

 

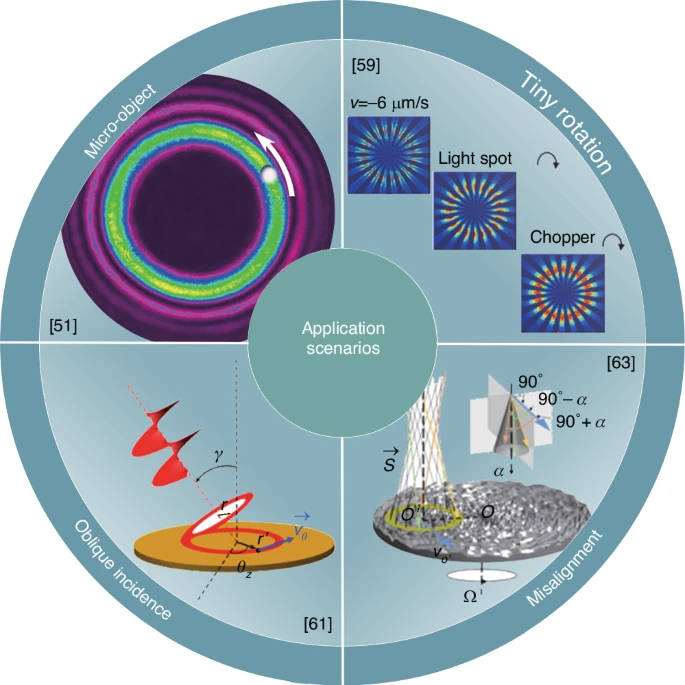
图5 旋转多普勒效应的计量学应用。基于涡旋光束的旋转多普勒效应计量技术展现出卓越的环境适应性，覆盖理想条件至复杂场景（如微物体旋转检测、微小转角、斜入射及横向偏移等）。

传统旋转多普勒效应技术要求光束轴与物体转轴对准，限制了非合作目标应用。最新进展表明，利用斜入射下中心频率的入射角不变性，可精确提取旋转速度；横向偏移系统中，中心旋转多普勒频移保持恒定，而频谱展宽与偏移距离成正比，为旋转目标信息提取提供新维度。非共轴入射下频谱展宽效应与轨道角动量模态分布变化，可通过相邻旋转多普勒效应信号频差确定旋转频率。

针对粗糙表面、径向周期性运动面、转子、理想螺旋桨及圆周进动等复杂旋转体与运动状态的检测需求，旋转多普勒效应测量技术正向高鲁棒性与高精度持续演进。贝塞尔-高斯光束、完美涡旋光束、环形艾里高斯涡旋光束、组合涡旋光束及碎片化光学涡旋等新型探针光束的应用，可提升信噪比、旋转速度测量精度及抗遮挡/远距适应能力。需指出，上述光束均设计为二维横向光场，而多维光场信息的深度开发有望实现全自由度运动解析。进一步探索融合时空维度的四维结构光，或将为超快动力学检测开辟全新路径。

除旋转多普勒频移外，涡旋光束的轨道角动量谱可直接作为探测复杂结构物体的有效工具，为评估光-机系统提供额外自由度与守恒量。在封闭系统中，轨道角动量守恒特性使探测光束轨道角动量谱的任何变化均能揭示相互作用系统的关键信息。利用涡旋光的轨道角动量谱革新了远距离目标信息获取方式，相较传统方法实现质的飞跃：通过涡旋光束照射复杂物体并解析轨道角动量谱中的运动学数据，研究人员可更精准评估物体的复杂结构与动态行为。

离散轨道角动量谱深度解析为获取物体多维度属性提供全面洞见，如图6所示。该技术可实现微纳尺度精密测量，并增强几何结构识别与运动状态分析能力。在光学计量中，涡旋光作为超高灵敏度探针，其轨道角动量谱为微纳尺度高精度测量提供核心数据支撑（图6a）：不同参数球状粒子对探测光束散射/反射产生的特征轨道角动量谱，为提取微米级介质球尺寸、位置、椭圆度及环境折射率等参数建立理论基础。涡旋光束还可提升亚纳米级台阶高度测量灵敏度，通过全数字化技术实现无需参考校准的实时可靠评估。

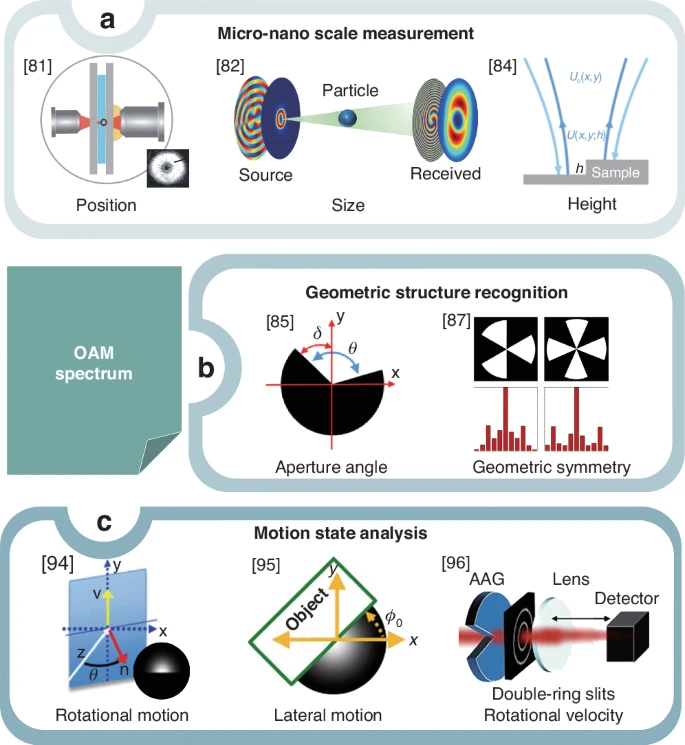
图6 探针光束轨道角动量谱在复杂物体评估中的应用。（a）微纳尺度高精度测量。独特轨道角动量谱提供额外自由度与守恒量，支撑微纳尺度精密测量。涡旋光作为超高灵敏度探针，其轨道角动量谱可解析亚纳米级形貌特征。（b）几何结构快速识别。通过关联轨道角动量强度谱极小值位置与物体孔径角、相位谱梯度与角向取向，实现几何参数快速精准测定。（c）运动状态解析。移动遮挡物引发的轨道角动量谱非对称性直接揭示物体旋转与横向运动，结合谱相位差可定量表征旋转动力学特性。

轨道角动量谱分析对复杂几何结构识别至关重要：轨道角动量强度谱凹陷位置直接关联物体孔径角，而轨道角动量相位谱梯度受物体角向取向影响（图6b）。该特性支持几何物体孔径角与取向同步测量，结合机器学习可优化方法体系，实现低计算成本的高效目标识别（仅需接收涡旋光束强度分布即可精确判定孔径角与取向）。基于轨道角动量谱的数字螺旋成像技术可实现几何结构快速精准识别。

数字螺旋成像实验证实，轨道角动量谱可成功实现物体几何对称性快速精确判定。该技术认为轨道角动量谱能重构任意图像，通过向各轨道角动量模式引入时变相位因子可实现图像旋转/反转等操作。相比傅里叶变换，拉盖尔-高斯模式谱在高速旋转下仍保持稳定，对快速旋转目标追踪极具价值。涡旋光旋转多普勒效应技术与轨道角动量谱分析相结合，在旋转图案几何对称性检测中成效显著：时空调控的非对称完美涡旋基可实现多样化脉冲序列设计，有效识别振幅目标并精准感知波前相位；轨道角动量扫描拓展提升方位分辨率，利用轨道角动量谱-方位角对偶性实现宽域精密测量。轨道角动量谱探针为复杂物体或旋转运动检测提供强健工具集，结合探针光束多维度数据可进一步强化性能。

运动状态解析方面，移动遮挡物引发的轨道角动量谱非对称性可直接指示目标横向运动（图6c），无需图像重建且仅需单光束即可完成运动检测。探测光束轨道角动量谱相位差与物体旋转取向成正比，类似斯托克斯偏振测量原理，可通过相位差判定旋转运动。单像素探测器记录相干-轨道角动量矩阵可简化轴对称物体角移/转速评估，深入解析光束或作用物体的方向特性。

天体物理尺度应用典型案例为黑洞探测。传统方法通过分析黑洞对邻近物质与光的作用（如光路方向与相位变化）推断其特性。轨道角动量观测技术的引入显著提升天体研究能力（尤其针对黑洞事件视界附近天体）。具有暗核特征的涡旋光束可增强微弱背景信号，实现精密天文测量。例如，光学涡旋日冕仪与自适应光学结合使双星系统主星亮度抑制率达97%，基于此，阿夏戈122 cm望远镜利用星光成功生成并研究l=1级光学涡旋。

多点干涉仪技术通过探测天体电磁波中光学涡旋的轨道角动量，推动天体物理学发展，为黑洞探索开辟新途径。精确测量黑洞引发的相位与波前畸变，可通过轨道角动量谱直接观测预言并确认旋转黑洞存在。观测技术进步支持更复杂的旋转黑洞测量验证，如利用M87黑洞周围爱因斯坦环亮度温度公开图像重构轨道角动量与电磁涡度，如图7所示。轨道角动量提供的附加信息不仅可判定致密天体真实转速，更使科学家能以旋转黑洞为实验室检验广义相对论原理。需指出，此类毫米波观测受大气湍流影响微乎其微，可忽略不计。

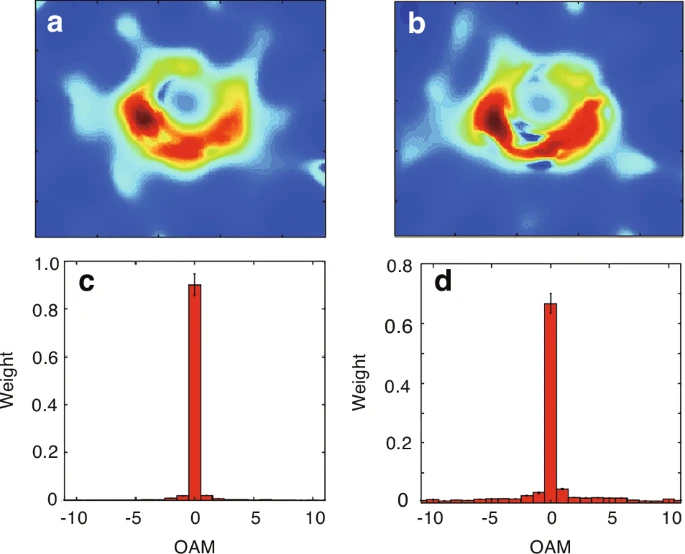
图7 黑洞爱因斯坦环扭曲波观测。（a）与（b） 通过有限频段亮度温度强度传输方程重建的电场分量归一化幅度，分别对应第一阶段与第二阶段数据。（c）与（d） 相应轨道角动量谱分析。

涡旋光束通过光-物质相互作用揭示复杂介质动力学特性，其独特传输特性使其成为多种环境遥感的高效工具，可检测流体速度、温度、湿度、密度、折射率、湍流及悬浮颗粒散射等参数的细微变化。研究涡旋光在复杂介质中的传播特性，可为介质参数分类与反演提供技术支撑。结合深度学习算法，显著提升涡旋光数据分析能力：通过解析复杂数据模式与关联性，增强环境评估与监测的精度与广度。这种技术协同不仅优化测量精度，更拓展了多领域应用潜力。

大气环境监测中，涡旋光束因其强度/相位结构独特性及携带的轨道角动量特性，对大气折射率微小变化高度敏感，成为探测湍流参数的有效工具，如图8所示。其在传输过程中受大气扰动导致强度分布破裂形成散斑图样——这些散斑蕴含丰富大气信息，是提取湍流特征参数的关键。通过神经网络模型处理散斑图样（特别是校正受扰涡旋光束的湍流像差并识别其在大气中携带的轨道角动量模式），显著降低了湍流不利影响。

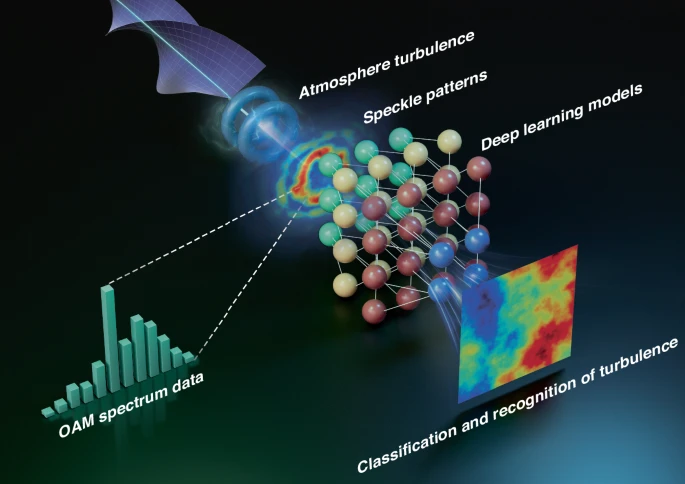
图8 基于涡旋光传播特性的大气环境监测增强技术。涡旋光束大气传输过程中，湍流扰动导致其强度分布破裂、螺旋相位结构畸变，形成散斑图样并引发轨道角动量谱展宽。分析这些效应可反演大气特性参数，结合二维散斑图与一维轨道角动量谱数据，深度学习模型能精确分类与重建湍流大气状态。

基于卷积神经网络的自适应大气像差校正新方法，通过分析不同大气条件下涡旋光束散斑图样推导泽尼克多项式系数，为湍流像差补偿提供新思路。改进的深度卷积神经网络模型可同时补偿多束畸变涡旋光束，关联散斑图样与大气湍流像差，显著提升轨道角动量模式纯度。通过解析涡旋光穿越大气湍流产生的散斑特征确定湍流参数，如图9所示，优化像差校正策略。卷积神经网络像差校正模型有效抑制大气湍流，大幅提升矢量涡旋光束相位分布传输质量与轨道角动量模式纯度。

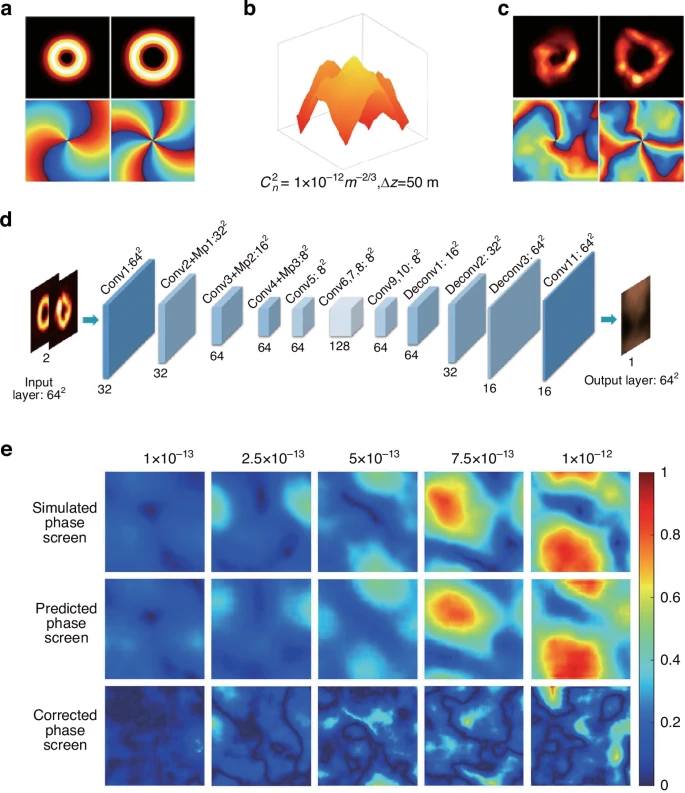
图9 基于涡旋光散斑图样的大气参数反演与校正。（a）未受扰动光束强度与相位分布。（b）模拟大气湍流等效相位屏。（c）扰动后涡旋光束强度与相位分布。（d）卷积神经网络湍流补偿框架示意图。（e）不同湍流强度下模拟/预测/补偿相位屏对比。

人工神经网络技术的应用使大气湍流中16个重叠轨道角动量模式识别准确率达98.3%。全连接神经网络对高阶多模涡旋光束检测表现出强鲁棒性，即使在低信噪比下对110种多模涡旋光束仍保持74%以上分类准确率。卷积神经网络算法集成推动自适应解调器发展，无需额外硬件即可精准识别不同轨道角动量模式涡旋光。光学反馈网络通过训练卷积神经网络模型分析受扰涡旋光散斑，动态调控不同湍流条件下的轨道角动量模式分布，使其匹配目标图样。深度前馈神经网络策略对混合态涡旋光轨道角动量模式检测精度超99%（即使在千米级大气湍流中）。将后干涉与原始强度图样融合至卷积神经网络框架，大幅提升湍流中轨道角动量模式识别能力。基于卷积神经网络分析受扰涡旋光散斑，成功提取大气湍流信息并校正像差、识别轨道角动量模式。散斑与轨道角动量谱数据融合显著提升大气湍流中轨道角动量模式检测效率与精度。

大气湍流分类研究取得重要进展。通过分析涡旋光大气传输散斑图样，系统分类并重建六种主要湍流等级。LeNet-5 神经网络对五类湍流强度的分类与重建表现出色。支持向量机利用闪烁指数、束宽、光束漂移等特征分类与反演大气环境参数，高效识别涡旋光轨道角动量模式。迁移学习框架下ResNet-101模型能精准识别涡旋光轨道角动量模式及传输距离（适应不同湍流条件）。

另一方面，大气湍流会扭曲涡旋光束螺旋相位结构，引发轨道角动量模式串扰与谱展宽（图8）。分析受扰涡旋光轨道角动量谱可揭示其大气传输特性，为反演湍流参数提供独特途径（该潜力尚未充分挖掘）。基于多模贝塞尔-高斯光束的纵向结构光传输，如图10所示，可根据传输距离与湍流强度引起的束宽变化及轨道角动量模式耦合效应，精确测量接收端湍流诱导的轨道角动量模式功率耦合，推导传播路径上的湍流强度分布（10公里距离内湍流结构常数波动达30 dB时仍保持稳定检测精度）。

利用受扰涡旋光轨道角动量谱数据训练支持向量机模型，可独立测定大气湍流雷诺数与Fried参数，同步评估温度、风速等实验参数变化。相较基于闪烁指数的传统技术，轨道角动量谱探针测量温度与风速性能优势显著。涡旋光大气传输散斑图样及其展宽轨道角动量谱蕴含多尺度大气特征信息：散斑反映局部大气细节，轨道角动量谱揭示全局大气结构。传统机器学习方法多单独分析畸变强度或相位（如轨道角动量）信息，而将两类数据集融合（或整合受扰涡旋光其他特征数据）形成的多尺度特征融合策略，可显著提升大气参数分类与反演的精度、准确度及训练速度。

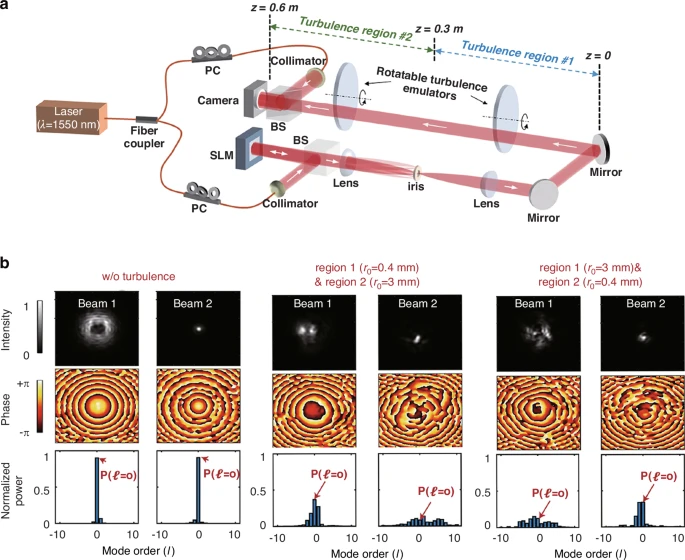
图10 双湍流区域束宽测量与模态耦合实验结果。（a）实验装置采用两束纵向结构光束（0<z<0.3m与0.3m<z<0.6m束宽分别收窄）。（b）实验测得的强度/相位分布及Beam 1-2的归一化模态谱（区域1-2采用不同r₀湍流参数）。

04

基于涡旋光轨道角动量模式的量子传感

经典光学计量学中，中心极限定理指出：通过n次重复测量取平均，可将统计误差降至与n^-1/2成正比。而新兴的量子计量学突破经典限制，将误差降至与n^-1成正比，超越标准量子极限。这一突破依托量子资源的战略性应用。光子数路径纠缠态（定义为N个光子处于一路、零光子处于另一路的叠加态）成为量子计量基础，但其对损耗与噪声高度敏感（光子数增减导致N值变化，影响测量精度）。

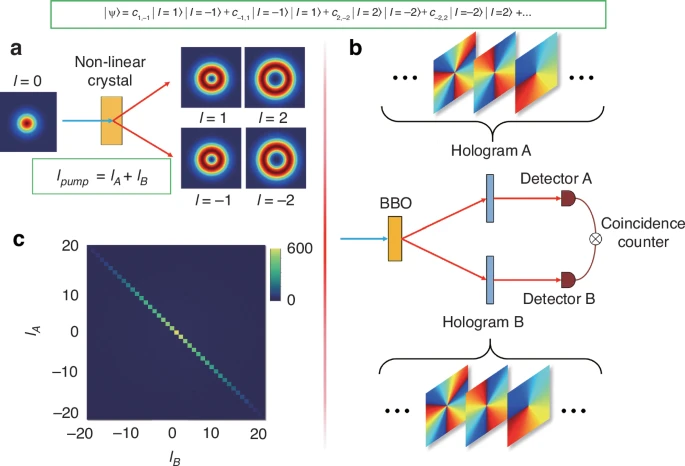
图11 轨道角动量纠缠产生与测量。（a）非线性晶体中自发参量下转换产生轨道角动量纠缠。（b）测量过程采用量子化模态分解法。空间光调制器加载全息图，单模光纤耦合后符合计数检测。（c）实验证实轨道角动量自然形成施密特基，验证单光子层面轨道角动量守恒。

^{二十年前，轨道角动量作为纠缠态基矢的实验验证开启新纪元。经典轨道角动量态通过光源内/外调制产生并检测，其生成与探测过程分离；量子轨道角动量纠缠态则遵循量子力学"测量即存在"原则，通过后选择实现。典型轨道角动量纠缠实验（图11a）中，高能光子穿过非线性晶体发生自发参量下转换，产生两低能纠缠光子。其位置与线动量纠缠，而单光子层面轨道角动量守恒使量子态亦可表达为轨道角动量基矢形式。例如，泵浦光子轨道角动量为零时，光子A与B的轨道角动量代数和必为零，形成量子态：}

通过逆向生成步骤耦合单模光纤（单光子轨道角动量敏感探测器）测量各光子，并符合计数揭示量子关联特性（图11b）。此类终态可用于高维量子协议，其自然施密特基构成的高维态实验实例如图11c所示。该发现为研究人员开辟了广阔的高维希尔伯特空间（理论轨道角动量值域从−∞延伸至∞），引发学界高度关注。

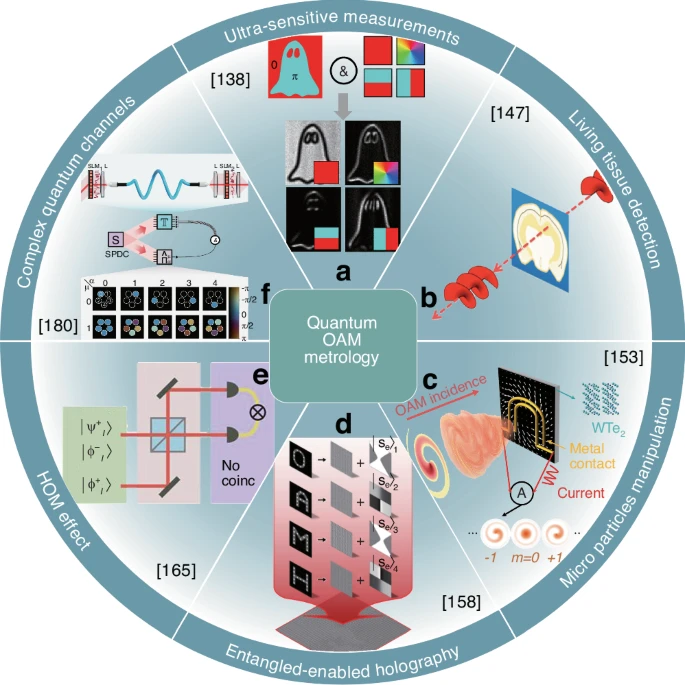
图12 量子轨道角动量计量学前沿应用。（a）物理量超精密测量。量子轨道角动量态实现精度与灵敏度突破。（b）活体组织量子成像。轨道角动量量子态用于生物组织深层探测。（c）微观粒子操控。轨道角动量光束与粒子相互作用实现精密调控。（d）纠缠全息成像。纠缠光子对生成高分辨率全息图，提升成像景深与清晰度。（e）HOM效应量子态分辨。基于Hong-Ou-Mandel效应的量子态精准鉴别，推动量子计算发展。（f）复杂量子信道解析。量子通信信道特性精细表征，深化量子信息传输机制认知。

量子数字螺旋成像技术通过轨道角动量谱非局域分析物体特性：产生两轨道角动量纠缠光子，一束照射未知物体，另一束进行常规模态分解，关键点在于未与物体作用光子的轨道角动量谱测量。早期实验在物体光路引入分数轨道角动量相位掩模，现已优化为任意空间分辨相位调制，甚至应用于物理角缝检测。虽纠缠本身未直接提升分辨率，但结合轨道角动量谱分析与旋转频移可检测物理/相位物体旋转。

尽管存在局限，轨道角动量仍为旋转超灵敏测量提供可能（图12a）。考虑叠加态经历旋转θ后的终态，旋转增强因子表明：轨道角动量态呈现类光子数路径纠缠态干涉条纹，灵敏度提升l倍。该原理已通过路径纠缠轨道角动量光子验证，实现角位移测量的分辨率与灵敏度超越经典极限且增强因子在极高轨道角动量值时仍成立，由此提出"光子齿轮"概念。此类研究需轨道角动量轴与转轴严格对准，但通过构建马约拉纳星座轨道角动量，可实现转轴未知时的量子增强旋转测量。

传统观点认为轨道角动量对手性结构检测无直接贡献，但新研究揭示四极场关键作用，并成功利用轨道角动量光子探测活体组织（图12b）。尽管经典光与轨道角动量相互作用认知深化，量子层面进展有限。重要但被忽视的突破显示：多波长偏振纠缠光子对可高效测量手性分子光学活性，但量子轨道角动量态手性检测仍无进展。开发量子轨道角动量手性检测方法仍是待解难题，亟待科学界探索。

光与物质轨道角动量相互作用方面，轨道角动量向束缚电子转移的实验标志重大进展。单俘获离子价电子吸收单个光子的偏振角动量与空间结构（轨道角动量）角动量各一量子。该研究还解答"轴上无光场时如何传递轨道角动量"的难题，即关键在于场梯度而非场本身。该工作推动多项电子态操控突破（图12c）：基于光轨道角动量的轨道光电流效应、激发过程双量子路径相干调控诱导矢量电流、轨道角动量印迹于传播电子物质波引发轨道角动量依赖二向色光电效应。这些进展孕育新型单光子电子谱学，或应用于轨道角动量光控化学。

纠缠全息技术作为新兴应用（图12d），凭借对经典噪声的强抗扰性，为样本远程分析与信息共享提供新途径。该技术可无缝对接传统全息应用领域（医学成像、安防、制造），其非局域特性使被测物与全息图可异地分布，开启全球协作新可能。

Hong-Ou-Mandel效应（图12e）作为经典量子计量资源，最初用于飞秒级时间测量，后扩展至阿秒级，并应用于量子显微术。在空间模式领域，HOM效应作为"秒表"探测飞行轨道角动量光子的相位差异，同时在轨道角动量量子态工程中用于态测量与滤波。

量子轨道角动量光探测复杂量子信道（图12f）是前沿方向：量子态与量子信道的同构性表明，对一者的测量等效于对另一者的测量。经典轨道角动量态在复杂信道中行为与量子态具相似性，该特性被创新性用于经典光增强量子过程，或量子工具解析经典态，催生"经典纠缠"新学科。

量子轨道角动量态不仅广泛用于量子通信，还可探测与传递复杂信道中的纠缠。纠缠衰减可直测量信道特性，结合高维轨道角动量实现系统并行探测。此类复杂系统天然适配机器学习与人工智能，既可校正输出态，亦可作为环境探针。反之，介质复杂性可策略性用于精密调控目标量子态与电路。

总之，研究人员系统综述了基于涡旋光束（以其独特螺旋相位结构与携带的轨道角动量轨道角动量为特征）的光学计量学重要进展。涡旋光束通过实现光与物质间高灵敏度手性相互作用探测、基于线性与旋转多普勒效应的三维运动精密检测等优势，显著拓展了光学计量应用边界。其在复杂介质探测方面表现卓越，应用于环境监测、深层组织成像及噪声信道通信等领域。通过融合复杂光场调控与人工智能技术，可进一步优化现有方法体系。涡旋光计量技术展现出变革性应用价值，为光学计量学的跨越式发展提供强劲驱动力。