干涉图样螺旋锥形光束的产生与重构
专家视点
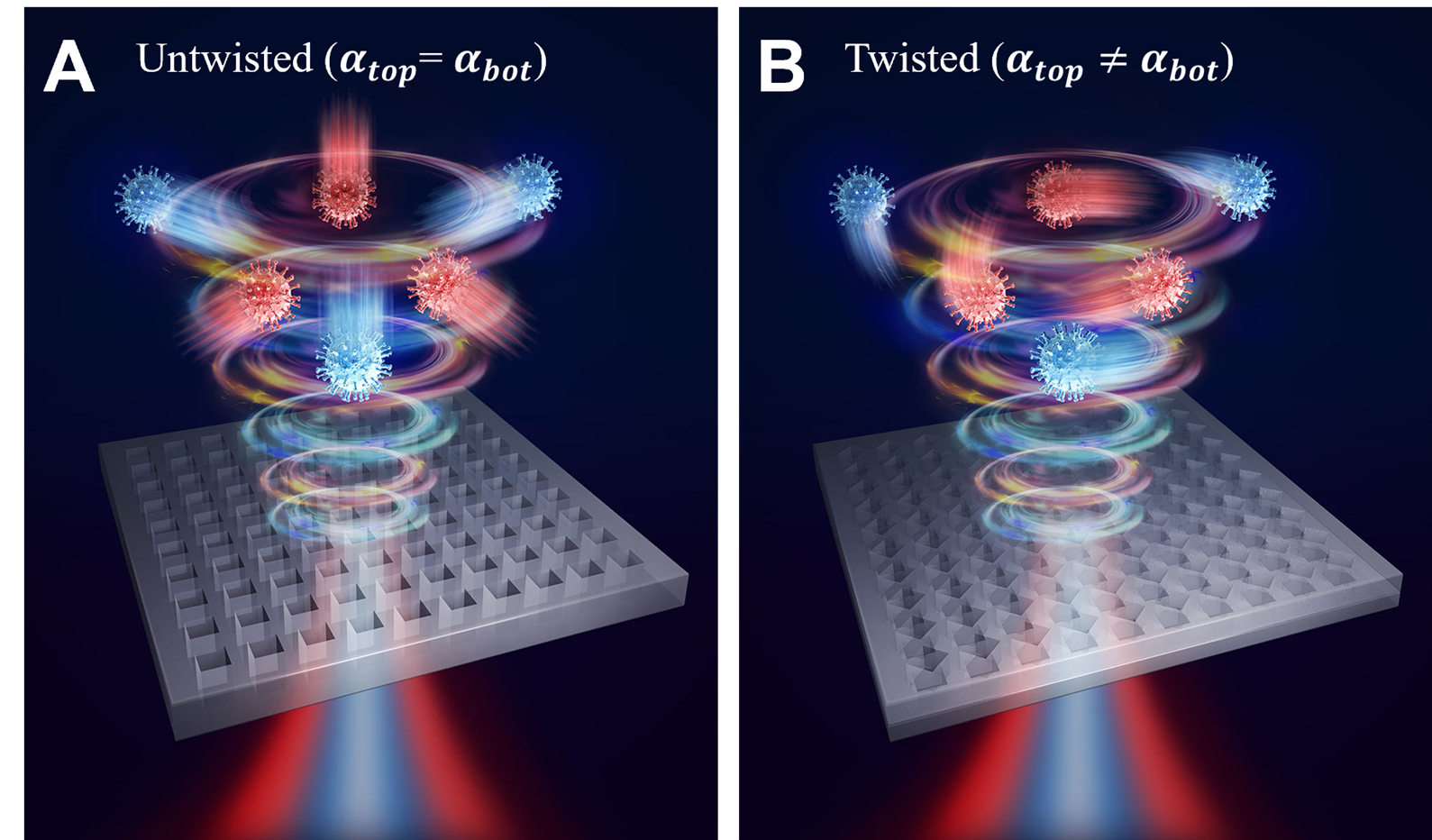
自2005年首次亮相以来,光学螺旋锥形光束在整个结构光领域引起了相当大的关注。螺旋锥光束可由螺旋和锥形相位函数的乘积产生,导致在经历傅里叶变换时焦平面处的螺旋强度分布。与拉盖尔-高斯光束和贝塞尔-高斯光束等传统涡旋光束不同,不可分离的径向和角相位分量将带来手性特征和独特的传播动力学,使得螺旋锥形光束在粒子操纵、纳米结构制造和光学计量领域成为潜在的候选者。在此,许东野等人从理论和实验上提出了一种产生干涉图样螺旋锥形光束的方法。通过利用复振幅调制和光学干涉技术,研究人员获得了具有复杂条纹结构的螺旋锥光束。为了精确控制光场分布,在螺旋锥相位表达式中操纵方位角项,以操纵场分布,从而给出了几个典型案例,突出了方法的多功能性。通过进一步的组合,研究人员实现了更复杂的综合螺旋锥形光束模式,以满足各种应用的要求。这项研究深化了对螺旋状光学图案的认识,并为潜在的应用开辟了新的途径,特别是在粒子操纵、纳米结构制造和光学计量领域。该工作发表在Chinese Optics Letters上。

Dongye Xu, Shaoxiang Duan, Xingyu Mao, Wenmin Ren, Yuan Yao, Wei Lin, Hao Zhang and Bo Liu, Generation and reconfiguration of interference-pattern helico-conical beams. Chin. Opt. Lett. 22(9): 090009 (2024).
最近,研究人员报道了更灵活螺旋锥形光束的产生和制造。例如,Cheng等人通过修改径向指数提出了一种新型的开度可控螺旋锥形光束;Hu等人开发了由具有不同方位角偏移因子的多个子螺旋锥形光束组成的多扭曲光束并实现了微球制导。此外,Segura等人开发了一个新的螺旋锥矢量光束族。同时,与螺旋锥相位相关的异常传播特性研究也逐渐出现。例如,Alonzo于2007年揭示了螺旋锥形光束的三维强度分布。然后,从理论和实验的角度报道了它们的自愈特性。在过去的几年里,研究人员还详细研究了具有混合螺旋锥相位的艾里光束和贝塞尔-高斯光束的聚焦和传播特性。然而,现有的大多数研究都是基于普通的螺旋锥相位。从更广泛的角度来看,由于其在工程中的灵活性,也有一些替代的光学配置,例如任意曲线光束和交叉相位结构。此外,作为当前热门的研究领域之一,大多数光学阵列都专注于传统的光学涡旋。尽管螺旋锥形光束的研究涉及各种阵列,但现有的螺旋锥形光束研究尚未进行进一步重建。因此,上述问题鼓励探索更复杂的螺旋锥形光束模式,以丰富结构光场的原理和应用。
光学螺旋锥形光束可以用螺旋的不可分离产物产生锥形相位函数。它的形式如下:
其中,(r, θ)表示极坐标,Φ是光场在初始平面Ψ(r, θ)中的相位分布,Φa(θ)=lθ和Φr (r)分别表示方位角和径向相位项。参数l是拓扑荷,r0是径向坐标的归一化因子,对应于入射光束孔径或半径宽度,K是一个常数,取0或1。方程式1中的相位表达式表明,在经历傅里叶变换时,焦平面处出现的光学螺旋锥形光束将产生螺旋强度图案。当K=1时,可以获得完整的螺旋图案,而当K=0时,只能获得截断图案。
然而,在之前研究中,螺旋锥形光束的曲线轨迹似乎总是狭窄而尖锐,如图1(a)所示。它限制了在现有模式的基础上进一步构建精细结构。一个潜在的解决方案是拓宽螺旋锥形光束的螺旋轨迹,以便创造空间来采用更多细节。它很容易引向傅里叶光学中的二维卷积定理:
其中(ρ, φ)表示观测平面上的极坐标,E(ρ, φ)=F(Ψ(r, θ))是光学螺旋锥形光束的复振幅分布,h(r, θ)是截断函数,H(ρ, φ)是相应的傅里叶变换,符号[*]表示卷积运算。方程2启发将h(r, θ)视为类高斯函数,其由下式给出:
其中,w0是高斯截断的半宽度。因此,hG(r, θ)的傅里叶变换仍是一个类高斯函数,卷积运算导致观测平面上的每个点都进行高斯型扩展,使曲线轨迹看起来更强,如图1(b)所示。此外,w0与实验装置中高斯光束半宽度完全对应。因此,可以通过调整初始平面中高斯截断的大小以及入射高斯斑的半径来控制螺旋锥形光束曲线轨迹的宽度。
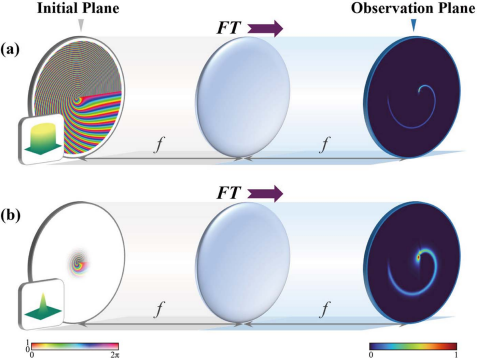
图1(a)原始螺旋锥形光束和(b)加宽螺旋锥形光束的生成示意图。FT:傅里叶变换;f:焦距。嵌入在初始平面中的插图表示截断函数。
制造精细结构的最常见策略之一是构建光学涡旋阵列,这意味着光学奇点根据光场的分布或其他预定义的轨迹排列。同样, 研究人员加不同拓扑荷的螺旋锥形光束,在光场的曲线轨迹上产生光学干涉条纹,可以表示为
其中,(l1,r0,1)和(l2,r0,2)分别是第一和第二光场分量的拓扑荷和归一化径向因子。值得注意的是,由于相位定义的不可分离性,参数l和r0同时影响螺旋锥形光束的规模。为了获得具有清晰可见干涉条纹的图案,假设通过保持比率l/r0将干涉分量拉伸到相同的尺寸。在光学相位分布方面,条纹的数量应由拓扑荷的差值决定,即Δl=l1−l2。由于螺旋锥形光束的固有手性特性,具有相同符号拓扑荷的光束与其具有相反符号拓扑荷的对应光束的干涉之间可能存在潜在差异。总之,通过调整l和r0的值,可以获得具有条纹结构的干涉螺旋锥形光束,条纹的数量和样式也是可调的。
然后,回顾一下方程式1。应当注意,方位角相位Φa(θ)与方位角呈线性关系。事实上,可通过重写初始平面中方位角和相位之间的关系来进一步改变螺旋锥形光束的配置。为了探索更多的重构模式,这里研究了三种携带非线性相位的情况,包括指数型、正弦型和啁啾振荡型情况,如图2所示。初始平面中指数型情况的相位分布表示为
其中,n是指数因子。图2(a)绘制了当n等于几个特定值时方位角相位Φa和θ之间的关系。原始线性关系也作为参考绘制,为简单起见,在与图2相关的连续部分中,l设置为1。当n从1减小到0时,螺旋锥形光束的开口收缩直到闭合,最终退化为环状模式。初始平面中正弦型情况的相位分布表示为:
其中,t是正弦函数的缩放因子。同样,图2(b)显示了不同t的方位角相位Φa和θ之间的关系。随着t从0.5增加到1,螺旋锥形光束的开口也会随着对称性的增强而减小,但不会完全闭合,这可以从图2(a)的演化趋势中推断出来。初始平面中啁啾振荡型情况的相位分布表示为:
其中,c是啁啾幅度因子,m是周期因子。如图2(c1)和2(c2)所示,c越大,相位振荡越强烈。系数m决定了循环次数,因为它在图2(c1)中设置为3,在图2中设置为5(c2)。在啁啾振荡型的情况下,螺旋锥形光束的曲线轨迹将折叠成m段,c值越大,其效果越明显。总之,可以通过调制方位角相位项来重新配置螺旋锥形光束模式,特别是对于曲线轨迹、开口尺寸和对称度等。
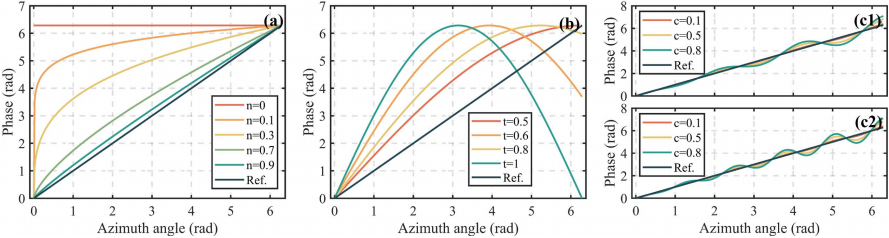
图2 对于不同的重新配置的螺旋锥形光束图案,方位相位Φa是方位角θ的函数。(a)指数型案例;(b) 正弦型案例;(c1)-(c2) 啁啾振荡型情况,(c1)中m=3,(c2)中m=5。
在上述讨论中,研究人员给出了单个螺旋锥形光束的重新配置。事实上,还可以通过平移、旋转和翻转等几何变换操作来改变图案的位置。根据傅里叶变换的特性,可以很容易地实现旋转和翻转。观测平面中的平移需要通过在初始平面中引入相移来实现,该相移由下式给出:
其中,X和Y是指初始平面中的笛卡尔坐标。平移因子SX和SY分别定义为焦平面内的位移除以透镜在X和Y方向上的波长和焦距。此外,还可以组合相同或不同的螺旋锥形光束,以进一步丰富模式的多样性。
为了验证上述理论分析,研究人员基于角谱传播算法对干涉图案螺旋锥形光束的图案分布进行数值模拟。图3展示出了用于产生和观察螺旋锥形光束的实验装置。高斯1064 nm激光束通过半波片和偏振器发射,使光学偏振态与空间光调制器匹配,以获得最大的调制效率。光束被调整为具有由L1和L2的组合确定的合适的横向尺寸,然后它穿过反射平面镜到达分束器。一个高斯模式分支由加载到仅反射相位液晶空间光调制器上的相位全息图调制。由L3和L4组成的4-f系统在傅里叶平面上的光圈辅助下滤除一阶衍射光束。透镜L5的前焦点与L4的后焦点重合,起到傅里叶透镜的作用。所需的螺旋锥形光束场分布可以通过电荷耦合器相机观察和捕获。
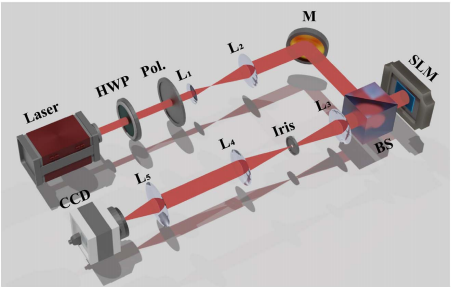
图3 实验装置示意图。HWP,半波片;PoL.,偏振器;L1-L5 ,透镜;M, 平面镜;SLM,空间光调制器(1920像素×1080像素,间距8 μm);BS,分束器;CCD、电荷耦合器件。
首先,关注由相同符号拓扑荷(S型)和相反符号拓扑荷(O型)组成的普通干涉图案螺旋锥形光束,如图4所示。除非特别说明,否则K设置为1,w0=1 mm。图4(a1)-4(a3)显示了S型情况下的相位叠加,拓扑荷差Δl=l1-l2分别等于2、3和4。相应的强度模式,如图4(b1)-4(b3)所示,而条纹的数量由最外层干涉条纹起点处的红点标记。可以看出,条纹数似乎与Δl的值完全相同,这与传统的轨道角动量模式干涉模式相似。此外,在S型的情况下,干涉条纹往往很模糊,曲线上似乎存在一系列“断裂点”。同样,O型情况下螺旋锥形光束干涉图的相位和强度分布分别如图4(a4)-4(a6)和4(b4)-4(b6)所示。这里Δl分别设置为4,5和6,它们也与条纹的数量完全对应。与前者相比,O型的条纹似乎更细。图4(c1)-4(c6)中的实验结果与上述模拟结果非常吻合。
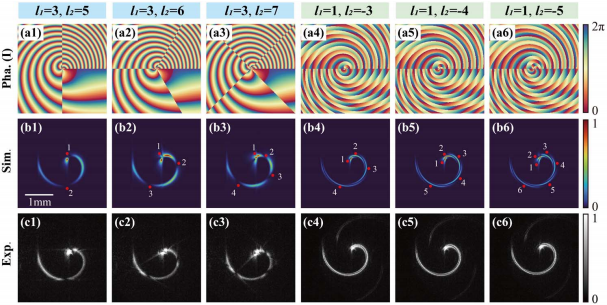
图4 普通干涉模式螺旋锥形光束。(a1)-(a6)初始平面中的相位分布;(b1)-(b6)观测平面内强度分布的数值模拟结果。红点表示条纹的数量。(c1)-(c6)对应于(b1)-(b6)的实验结果。
有必要给出导致S型和O型光束干涉条纹特性差异的明确原因。为了更好地比较,如图5所示,上述两种情况的拓扑荷差都设置为4。就螺旋锥形光束与相同符号拓扑荷的干涉而言,导致光学干涉的分量的Φa梯度都沿同一方向排列,如图5(a1)和5(a2)所示。否则,梯度将朝向相反的方向,如图5(b1)和5(b2)所示。在光学干涉方面,S型光束的干涉相位导致奇异点的出现,而O型光束的相干相位产生曲线相位分裂,分别如图5(a3)和5(b3)所示。
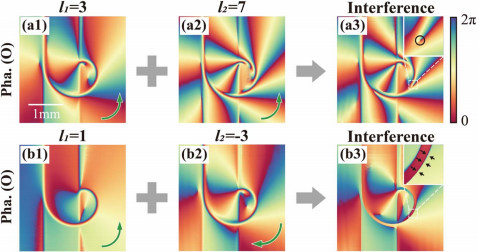
图5 观测平面内螺旋锥形光束的相位分布。(a1)-(a3) S型:l1=3,l2=7及其干涉图样。黑色圆圈标记奇点。(b1)–(b3) O型:l1=1,l2=−3及其干涉图样。黑色箭头标记奇点。绿色曲线箭头标记相位梯度。
除了条纹的特性外,通过调整方位相位项Φa的表达式,研究人员还展示了具有特殊曲线轨迹的更复杂的可重构干涉图案螺旋锥形光束。仿真和实验结果,如图6所示。首先,考虑指数型的情况。图6(a1)-6(a4)和6(c1)-6(c4)分别显示了S型(l1=3,l2=6)和O型(l1=1,l2=-3)情况下的干涉图案螺旋锥形光束,从左到右列的因子n分别设置为0.9,0.3,0.1和0。相应的实验结果分别如图6(b1)-6(b4)和6(d1)-6(d4)所示。可以看出,随着n的减小,螺旋锥形光束的开口变窄,直到完全闭合。应该指出的是,在这个过程中,条纹的数量也会减少。更有趣的是,当图案最终退化为标准环状光束时,S型情况根本不会留下条纹,如图6(a4)所示。然而,在O型情况下仍发现一条条纹,如图6(c4)所示。上述特征可解释如下:n的下降增强了初始螺旋锥形光束组分之间的相似性,消除了复合相的不连续性。然而,当n=0时,初始复合相分别退化为S型和O型光束锥形相和径向周期逆相。后者导致干涉图案中出现环状条纹,如图6(c4)和6(d4)所示。当涉及到正弦型情况时,以S型干涉情况为例(l1=3,l2=6)。图6(e1)-6(e4)和6(f1)-6(f4)给出了模拟和实验结果,从左到右的系数t分别设置为0.5,0.6,0.8和1。可以看出,随着t增加,螺旋锥形光束的开口会变窄,但不能完全关闭。此外,随着曲线轨迹的尾部向内卷曲,新的条纹出现了。根据图2(b),由于相位对称性,当t=1时,该模式最终充当字母“C”。啁啾振荡型情况的结果分别如图6(g1)-6(g4)和6(h1)-6(h4)所示,在这种情况下,以O型干扰为例(l1=1,l2=-3)。这里的啁啾相关因素如下:图6(g1)-6(h1)中的c=0.4,m=3,图6(g2)-6(h2)中的c=0.8,m=3。图6(g3)-6(h3)中的c+0.4,m=5以及图6(g4)-6(h4)中的c=0.8,m=5。由于周期振荡项引入的局部扰动,螺旋锥形光束的曲线轨迹包含(m-1)个拐点。此外,根据图2(c),随着参数c的增加,相位扰动将变得更强。从逻辑上讲,曲线轨迹更明显地弯曲了。
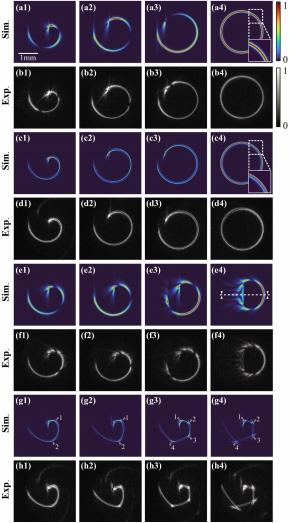
图6 复杂的干涉模式螺旋锥形光束。(a1)-(a4)指数型情况下的强度分布(l1=3,l2=6);(c1)-(c4) 指数型(l1=1,l2=-3)情况下的强度分布;(e1)-(e4) 正弦型(l1=3,l2=6)情况下的强度分布;啁啾振荡型(l1=1,l2=-3)情况下的(g1)-(g4) 强度分布;(b1)-(b4)、(d1)-(d4)、(f1)-(f4)和(h1)-(h4)分别显示了相应的实验结果。红色箭头表示膝点的数量。
通过前面描述的光场的灵活组合,研究人员获得了更复杂的螺旋锥形光束图案,如图7所示。图7(a1)和7(b1)显示了通过平移和翻转操作得到的“云”模式。此外,还可以使用由各种变换和组件组成的排列,如图7(a3)和7(b3)中的“海浪”模式以及图7(a4)和7(b4)的“蝴蝶”模式。

图7 干涉图案螺旋锥形光束的组合。(a1)“龙卷风”模式;(a2)“云”模式;(a3)“海浪”模式;(a4)“蝴蝶”图案;(b1)-(b4)分别显示了相应的实验结果。
总之,研究人员提出并实验生成了一种具有不同自由度可重构特性的干涉图螺旋锥形光束。利用光学干涉在螺旋锥形光束的曲线轨迹上产生了精细条纹,研究了相同或相反符号拓扑荷的干涉之间的差异。此外,研究人员展示了三种具有非线性方位角相位项的特殊图案,并讨论了曲线轨迹重构对光学复杂结构的影响。最后,通过几何变换操作实现了各种多螺旋锥形光束。具有柔性光场结构的螺旋锥光束有望在光学计量、多目标粒子操纵和纳米结构制造等领域得到应用。
免责声明:本文旨在传递更多科研资讯及分享,所有其他媒、网来源均注明出处,如涉及版权问题,请作者第一时间联系我们,我们将协调进行处理,最终解释权归旭为光电所有。